УДК 534.134:565.14  Ivan S. Maksymov, Andrey Pototsky Ivan S. Maksymov, Andrey Pototsky
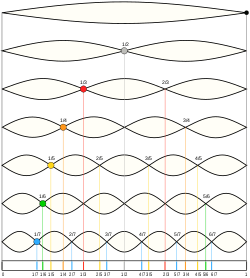
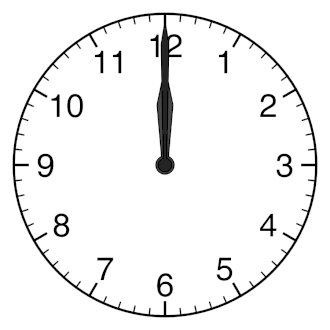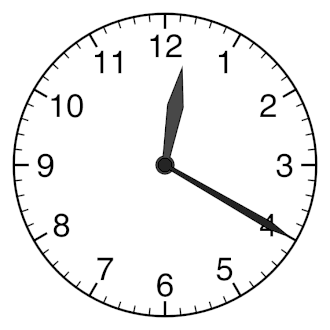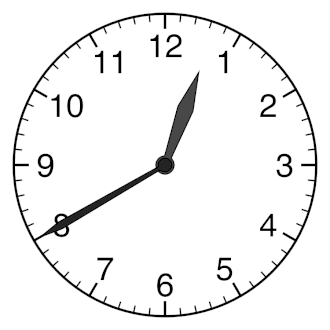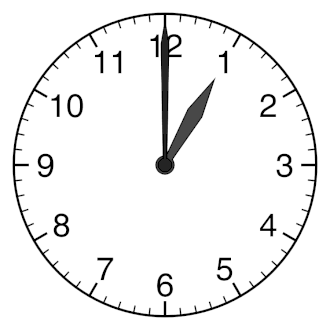
IntroductionVibrations and fluid-structure interactions are essential for efficient communication between living beings and they also underpin human-made imaging, spectroscopy and sensing techniques such as medical ultrasound and photoacoustic imaging modalities [1], Brillouin Light Scattering spectroscopy [2], and laser vibrometry [3] to name a few. Sound and vibrations are also likely to play an important role in the propagation of nerve impulses [4, 5] as well as they can be used to develop new methods of bacteria and virus killing [6, 7, 8]. Furthermore, using vibrations one could monitor, understand and control the behaviour of some animals, such as earthworms [9], and exploit them to sense and modify soil structure as well as to increase crop yields [10, 11, 12]. Earthworms – tube-shaped, segmented worms that have a world-wide distribution and are commonly found in soil – have become a subject of intensive research focused on their response to vibrations and sound. Some of these studies aim to explain the response of these animals to natural vibrations produced by predators, rain or plants [9]. Furthermore, the glial cell wrapping of the giant axons of earthworms resembles the myelin sheath of vertebrate nerve fibers [13]. Therefore, earthworms serve as a platform for neurobiological studies [14]. Earthworms are also cheap and using them does not require ethics approval. Hence, we choose these animals to demonstrate the onset of Faraday-like subharmonic body waves in a living organism subjected to external mechanical vibration. Classical nonlinear standing Faraday waves appear on the horizontal surface of an infinitely extended liquid supported by a vertically vibrating container [15]. For any given vibration frequency ω, when the vibration amplitude exceeds a certain critical value, the flat surface of the fluid becomes unstable and subharmonic surface waves oscillating at the frequency 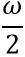 are formed. These oscillations are due to a parametric resonance between the forcing at the frequency ω and gravity-capillary surface waves with the dispersion relation Ω(k), being k a certain wave vector selected as Ω(k) = are formed. These oscillations are due to a parametric resonance between the forcing at the frequency ω and gravity-capillary surface waves with the dispersion relation Ω(k), being k a certain wave vector selected as Ω(k) = 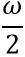 . . Faraday waves have become a paradigmatic example of nonlinear wave systems exhibiting complex periodic [16] and quasi-periodic [17, 18, 19] dynamics as well as chaotic behaviour [20, 21, 22, 23]. Recently, a number of applications of Faraday waves in the fields outside the area fluid dynamics have been suggested, including novel photonic devices [24, 25], metamaterials [26, 27], alternative sources of energy [28], and applications in biology [29]. Parametrically excited vibrations and surface waves have also been observed in isolated liquid drops subjected to external mechanical forcing [30, 31, 32, 33, 34, 35, 36, 37, 38]. In response to vibration, the drop can either adopt a regular star shape [30, 31, 32, 33] or exhibit a more dramatic transformation by spontaneously elongating in horizontal direction to form a worm-like structure of gradually increasing length [34, 35, 36, 37]. In contrast to the classical Faraday instability in infinitely extended systems, in isolated liquid drops the boundary conditions at the drop edge dictate the existence of a discrete set of vibrational modes [39, 40, 41, 42]. The eigenfrequency Ω of each mode depends on the boundary conditions at the contact line [40, 41]. When a drop is vibrated at the frequency ω, the fundamental subharmonic resonance occurs when the resonance condition Ω = 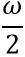 is fulfilled [30]. is fulfilled [30]. In inviscid fluids, the subharmonic response sets in at a vanishingly small vibration amplitude at frequencies that satisfy the resonance condition. For frequencies that do not satisfy the resonance condition, the critical amplitude is nonzero. In experiments with viscous isolated drops, the dependence of the subharmonic critical amplitude on the vibration frequency ω was shown to exhibit periodic variations [30, 32, 33]. This feature is in stark contrast with the Faraday instability in infinitely extended fluids, where the critical amplitude monotonically increases with the driving frequency ω [43]. In this work, we observe experimentally the subharmonic oscillations of the body of living earthworms lying horizontally on a flat solid surface subjected to vertical vibration. We measure the critical amplitude of the onset of subharmonic response as a function of the vibration frequency f, and we reveal that the obtained dependence exhibits signature characteristics of parametrically excited capillary surface waves in vibrated liquid drops [30, 31, 32, 33]. In particular, we show that the critical amplitude varies periodically with f. We explain the observed results by modelling the body of the worm as a horizontally-extended, liquid-filled elastic cylinder subjected to vertical vibration. Because the excitation of Faraday-like waves in living organisms has thus far received little attention [44], our findings promise to push the frontiers of our knowledge of fundamental nonlinear phenomena and chaotic behaviour in biological systems. For instance, our results should be qualitatively reproducible in other living systems such as bacteria, biological cells or individual organs in the body including the brain and blood vessels.
 Experimental resultsWe tested four different earthworm species encountered in the south eastern regions of Australia [45]. To correctly identify the earthworm species, we used an earthworm identification guide [46]. Eisenia fetida earthworms were purchased from a local fishing goods store, and on average they were 100 – 120 mm long and 5 – 6 mm wide. Lumbricus terrestris earthworms were harvested in the field and closely related to them Lumbricus rubellus earthworms were obtained from a local compost worm supplier. In this group, we selected the worms that measured approximately 120 – 150 mm in length and 8 – 10 mm in width. Several smaller 6 – 8-mm-long and 2 – 3-mm-wide Aporrectodea caliginosa earthworms were also harvested in the field and outcomes of their test were qualitatively similar. Earthworms are non-regulated animals, and therefore this research did not require the approval of our Institutional Animal Ethics Committee. However, the worms were treated as humane as practical and afterwards they were placed into a worm farm where they fully recovered. In preparation for experiments, earthworms were first placed in 20% ethanol for approximately 2 minutes, which immobilised them to simplify handling. Then, the entire body of an immobilised worm was placed on top of a thin Teflon plate that was vertically vibrated with the harmonic frequency f. The vibrations were detected by using an in-house laser vibrometry setup [38] consisting of a red laser diode and a photodetector. The intensity of light reflected from the worm is modulated due to the vertical vibration as well as the onset of parametrically excited body waves. We recorded these signals with Audacity software and Fourier-transformed them with Octave software to obtain frequency spectra. When required, the skin of the worm was moistened with water to avoid drying. However, in those cases special care was taken to remove all liquid drops from the Teflon plate. This ensured that Faraday waves are not excited on the liquid drop surface [38] and also dramatically simplified the analysis of the results.
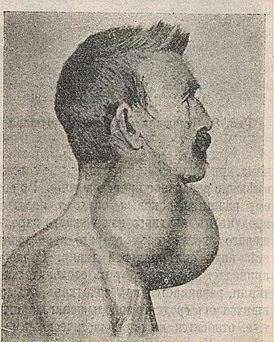
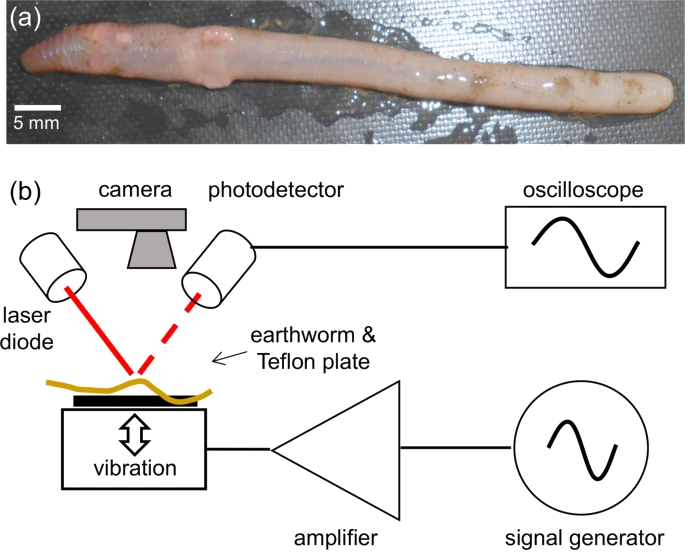 (a) Photograph of an anaesthetised Eisenia fetida earthworm. (b) Schematic of the experimental setup. A subwoofer covered by a thin Teflon plate is used as the source of vertical vibration. The sinusoidal vibration signal of frequency f is synthesised with a digital signal generator and amplified with an audio amplifier. Vibrations of the earthworm placed horizontally on top of the Teflon plate are measured by using a continuous wave red laser diode and a photodetector. The detected signals are visualised with an oscilloscope and sent to a laptop for post-processing. A digital camera is used to continuously monitor the position of the worm. 
Ivan S. Maksymov, Andrey Pototsky. Excitation of Faraday-like Body Waves in Vibrated Living Earthworms. Page 1 2 3 4 5 | References1. Emelianov, S. Light, sound, nanobubbles: New approach to contrast-enhanced ultrasound and photoacoustic imaging. J. Acoust. Soc. Am. 145, 1779 – 1779. ◄ 2. Ballmann, C. W., Meng, Z. & Yakovlev, V. V. Nonlinear brillouin spectroscopy: what makes it a better tool for biological viscoelastic measurements. Biomed. Opt. Express 10, 1750 – 1759. ◄ 3. Blamey, J., Yeo, L.Y. & Friend, J.R. Microscale capillary wave turbulence excited by high frequency vibration. Langmuir 29, 3835 – 3845. ◄ 4. Heimburg, T. & Jackson, A.D. On soliton propagation in biomembranes and nerves. PNAS 102, 9790 – 9795. ◄ ► ► 5. Hady, A.E. & Machta, B.B. On soliton propagation in biomembranes and nerves. Nat. Commun. 6, 6697. ◄ ► ► 6. Zinin, P.V., Allen, J.S.III & Levin, V.M. The mechanical resonances of bacteria cells. Phys. Rev. E 72, 61907. ◄ 7. Ivanova, E.P. et al. Bactericidal activity of black silicon. Nat. Commun. 4, 2838. ◄ 8. Boyd, B., Suslov, S.A., Becker, S., Greentree, A.D. & Maksymov, I.S. Beamed UV sonoluminescence by aspherical air bubble collapse near liquid-metal microparticles. Sci. Reps. 10, 1501. ◄ 9. Mitra, O., Callaham, M.A., Smith, M.L. & Yack, J.E. Grunting for worms: seismic vibrations cause Diplocardia earthworms to emerge from the soil. Biol. Lett. 5, 16 – 19. ◄ ◄ 10. Blakemore, R. & Hochkirch, A. Restore earthworms to rebuild topsoil. Nature 545, 30. ◄ 11. Lacoste, M., Ruiz, S. & Or, D. Listening to earthworms burrowing and roots growing-acoustic signatures of soil biological activity. Sci. Reps. 8, 10236. ◄ 12. Ruiz, S.A. & Or, D. Biomechanical limits to soil penetration by earthworms: direct measurements of hydroskeletal pressures and peristaltic motions. J.R. Soc. Interface 15, 20180127. ◄ ► 13. Roots, B.I. & Lane, N.J. Myelinating glia of earthworm giant axons: Thermally induced intramembranous changes. T issue Cell 15, 695 – 509. ◄ 14. Shannon, K.M., Gage, G.J., Jankovic, A., Wilson, W.J. & Marzullo, T.C. Portable conduction velocity experiments using earthworms for the college and high school neuroscience teaching laboratory. Adv. Physiol. Educ. 38, 62 – 70. ◄ ► ► ► 15. Faraday, M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. Royal Soc 121, 299 – 340. ◄ 16. Benjamin, T.B., Ursell, F.J. & Taylor, G.I. The stability of the plane free surface of a liquid in vertical periodic motion. Proc. Royal Soc. Lond. A 225, 505 – 515. ◄ 17. Henderson, D.M. & Miles, J.W. Single-mode faraday waves in small cylinders. J. Fluid Mech. 213, 95 – 109. ◄ 18. Miles, J.W. Nonlinear Faraday resonance. J. Fluid Mech. 146, 285 – 302. ◄ 19. Jiang, L., Ting, C.-L., Perlin, M. & Schultz, W.W. Moderate and steep faraday waves: instabilities, modulation and temporal asymmetries. J. Fluid Mech. 329, 275 – 307. ◄ 20. Punzmann, H., Shats, M. G. & Xia, H. Phase randomization of three-wave interactions in capillary waves. Phys. Rev. Lett. 103, 064502. ◄ ► 21. Xia, H., Maimbourg, T., Punzmann, H. & Shats, M. Oscillon dynamics and rogue wave generation in faraday surface ripples. Phys. Rev. Lett. 109, 114502 ◄ ► 22. Shats, M., Punzmann, H. & Xia, H. Capillary rogue waves. Phys. Rev. Lett. 104, 104503. ◄ 23. Shats, M., Xia, H. & Punzmann, H. Parametrically excited water surface ripples as ensembles of oscillons. Phys. Rev. Lett. 108, 034502. ◄ 24. Tarasov, N., Perego, A.M., Churkin, D.V., Staliunas, K. & Turitsyn, S.K. Mode-locking via dissipative faraday instability. Nat. Commun. 7, 12441. ◄ 25. Huang, S.-W. et al. Multispectral optical frequency comb based on microresonator faraday instability. In Frontiers in Optics 2017, FTu5A.3. ◄ 26. Domino, L., Tarpin, M., Patinet, S. & Eddi, A. Faraday wave lattice as an elastic metamaterial. J. Appl. Phys. 93, 050202. ◄ 27. Francois, N., Xia, H., Punzmann, H., Fontana, P. & Shats, M. Wave-based liquid-interface metamaterials. Nat. Commun. 8, 14325. ◄ 28. Alazemi, S., Lacarbonara, W. & Daqaq, M.F. Harvesting energy from Faraday waves. J. Appl. Phys. 122, 224501. ◄ 29. Sheldrake, M. & Sheldrake, R. Determinants of Faraday wave-patterns in water samples oscillated vertically at a range of frequencies from 50 – 200 Hz. Water 9, 1 – 27. ◄ 30. Yoshiyasu, N., Matsuda, K. & Takaki, R. Self-induced vibration of a water drop placed on an oscillating plate. J. Phys. Soc. Jpn. 65, 2068 – 2071. ◄ ◄ ◄ ◄ ◄ ► ► ► ► 31. Noblin, X., Buguin, A. & Brochard-Wyart, F. Vibrations of sessile drops. Eur. Phys. J. Spec. Top. 166, 7 – 10. ◄ ◄ ◄ ► ► ► 32. Ma, X., Liétor-Santos, J.-J. & Burton, J.C. Star-shaped oscillations of leidenfrost drops. Phys. Rev. Fluids 2, 031602. ◄ ◄ ◄ ◄ ► ► ► 33. Ma, X. & Burton, J.C. Self-organized oscillations of leidenfrost drops. J. Fluid Mech. 846, 263 – 291. ◄ ◄ ◄ ◄ ► ► ► 34. Hemmerle, A., Froehlicher, G., Bergeron, V., Charitat, T. & Farago, J. Worm-like instability of a vibrated sessile drop. Europhys. Lett. 111, 24003. ◄ ◄ 35. Pucci, G., Fort, E., Ben Amar, M. & Couder, Y. Mutual adaptation of a Faraday instability pattern with its flexible boundaries in floating fluid drops. Phys. Rev. Lett. 106, 024503. ◄ ◄ 36. Pucci, G., Ben Amar, M. & Couder, Y. Faraday instability in floating liquid lenses: the spontaneous mutual adaptation due to radiation pressure. J. Fluid Mech. 725, 402 – 427. ◄ ◄ 37. Pototsky, A. & Bestehorn, M. Shaping liquid drops by vibration. Europhys. Lett. 121, 46001. ◄ ◄ 38. Maksymov, I.S. & Pototsky, A. Harmonic and subharmonic waves on the surface of a vibrated liquid drop. Phys. Rev. E 100, 053106. ◄ ◄ ◄ ► ► ► ► ► 39. Bostwick, J.B. & Steen, P.H. Dynamics of sessile drops. Part 1. Inviscid theory. J. Fluid Mech. 760, 5 – 38. ◄ 40. Chang, C.-T., Bostwick, J.B., Daniel, S. & Steen, P.H. Dynamics of sessile drops. Part 2. Experiment. J. Fluid Mech. 768, 442 – 467. ◄ ◄ 41. Bostwick, J.B. & Steen, P.H. Dynamics of sessile drops. Part 3. Theory of forced oscillations. ◄ ◄ 42. Chang, C.-T., Bostwick, J.B., Steen, P.H. & Daniel, S. Substrate constraint modifies the Rayleigh spectrum of vibrating sessile drops. Phys. Rev. E 88, 023015. ◄ 43. Kumar, K. Linear theory of Faraday instability in viscous liquids. Proc. Royal Soc. Lond. A 452, 1113 – 1126. ◄ 44. Hong, S.-H. et al. Wave-controlled bacterial attachment and formation of biofilms. arXiv e-prints arXiv:1910.13004, 1910.13004. ◄ ► 45. Baker, G.H., Brown, G., Butt, K., Curry, J.P. & Scullion, J. Introduced earthworms in agricultural and reclaimed land: their ecology and influences on soil properties, plant production and other soil biota. Biol. Invasions 8, 1301 – 1316. ◄ 46. Earthworm Identification Guide for the OPAL Soil and Earthworm Survey, www.opalexplorenature.org. ◄ 47. Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates. ► ► |