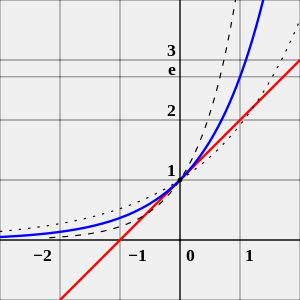
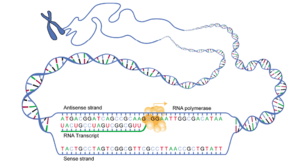
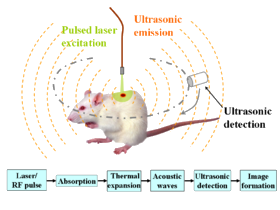
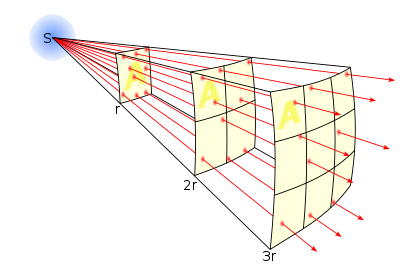
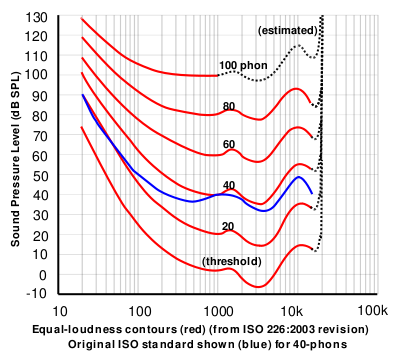
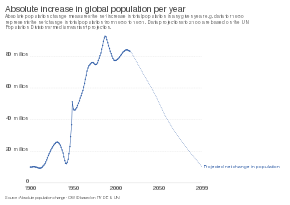
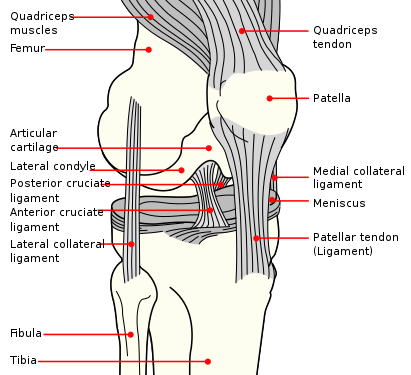
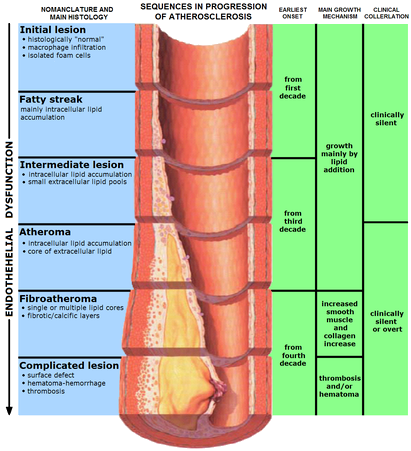
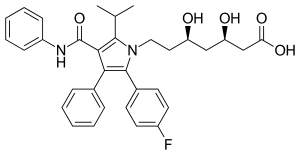
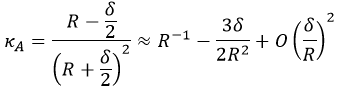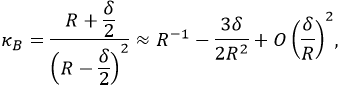Ivan S. Maksymov, Andrey Pototsky Ivan S. Maksymov, Andrey Pototsky
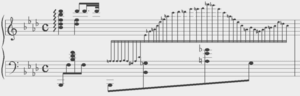
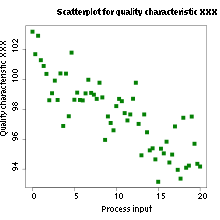
As a next step, we measure the lowest value of the vibration amplitude at which the subharmonic response of the worm body sets in. We call this value the critical amplitude and we plot it in Fig. 4 as a function of the frequency f for an Eisenia fetida worm. To obtain consistent results, we illuminated the same part of the body of the worm and we also established that the critical amplitude was unaffected by the intensity of the laser beam and the diameter of the laser spot. Significantly, in the investigated frequency range, the response of the Teflon plate to vertical vibrations is essentially uniform within the margin of error and also it is linearly proportional to the acoustic response of the subwoofer. The amplifier of the subwoofer also operates in the linear regime that allows us to use its input as a measure of the vibration amplitude. Thus, the measured critical amplitude is based on the input of the subwoofer, it does not require normalisation on the response of the Teflon plate and therefore its variations with the frequency are attributed solely to the response of the worm.
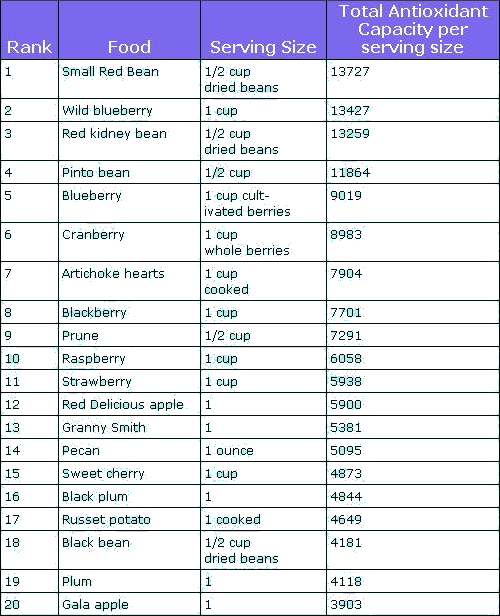
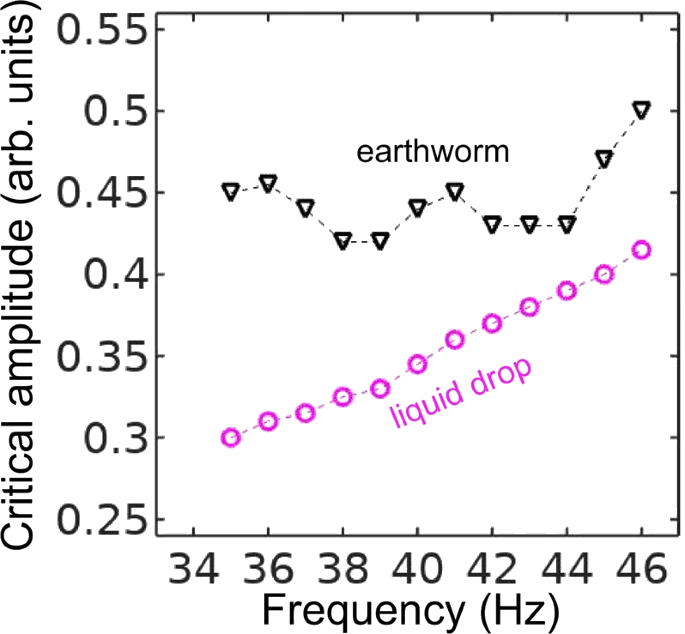 Critical vibration amplitude of the onset of the subharmonic response in an earthworm and a pancake-like canola oil drop plotted as a function of the vertical vibration frequency f. The dashed lines are the guide to the eye. Whereas in the selected frequency range the response of the canola oil drop is quasi-monotonic, the curve for the critical amplitude for the worm exhibits oscillations. These oscillations allow us to correlate the experimental data with the predictions of our theoretical model. In the 35 … 45 Hz frequency range, the critical amplitude is relatively low and therefore the body of the worm does not shift along the surface of the Teflon plate, thereby allowing us to obtain accurate results. In the critical amplitude dependence for the worm, we observe oscillations with the two minima at f ≈ 38 Hz and f ≈ 43 Hz. In contrast, the critical amplitude of an approximately 6 × 6 cm pancake-like drop of canola oil is quasi-monotonic in the 35 … 45 Hz range. A similar nonmonotonic dependence of the critical amplitude on the vibration frequency was previously observed in infinitely extended viscoelastic films [54]. In contrast to liquid drops of simple Newtonian fluids [38], the nonmonotonic dependence originates from the ability of a viscoelastic material to remember past stresses. Thus, in the Maxwell model of linear elasticity, the instantaneous stress in the material is described by a time-dependent relaxation modulus decaying over a characteristic relaxation time. The coupling between the period of forcing with the relaxation time of the material viscoelastic response leads to the oscillation of the critical amplitude as the function of the vibration frequency. Based on our experimental data, it is not possible to conclude whether the nonmonotonic dependence in Fig. 4 is due to viscoelastic properties of the skin of the worm, the finite size of the worm body or a combined effect of viscoelastic properties of the skin and the geometry of the worm. In the following, we assume that, similar to small liquid drops [30, 31, 32, 33], the nonmonotonic subharmonic response of the worm originates from the discrete spectrum of its natural vibration frequencies. We also develop a theoretical model considering the worm as an elastic cylindrical shell filled with an incompressible fluid, and we correlate the experimental results with the theoretical predictions.
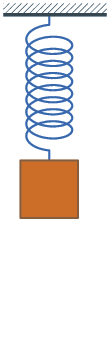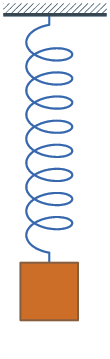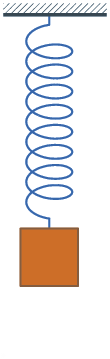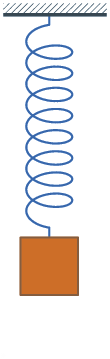
 Theoretical modelThe observed subharmonic oscillations of the earthworms bear a striking resemblance to the well-known phenomenon of parametrically excited capillary surface waves in vertically vibrated liquid drops [30, 31, 32, 33, 55]. To understand the physical origin of the subharmonic response of earthworms, we neglect the damping effect of the viscosity and model the body wall of the worm as an elastic cylindrical shell of length L with the Young’s modulus E, radius R and shell thickness H. The cylinder is filled with incompressible and inviscid fluid with the density ρl. An elastic cylindrical shell model of the worm body has been previously used to analyse the pressure exerted by earthworms during their burrowing activity [12]. When such a cylinder with the horizontally oriented axis is supported by a solid plate, its cross-sectional shape is no longer circular due gravity deformation. To estimate the squashing depth δ that measures the change in the vertical height of the cylinder in the squashed state, we neglect the bending energy of the thin shell as compared with the energy due to stretching. In this case, the equilibrium shape of the gravity deformed cross-section of the cylinder filled with an incompressible fluid of density ρl can be found by balancing the tension T per unit axial length of the elastic shell with the hydrostatic pressure [56]. In particular, we obtain ρlgH = T(κB − κA), where H is the height difference between the points A and B in Fig. 5 and κA,B denotes the curvature of the shell at the points. Assuming weak deformation such that 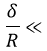 1, we approximate the shape of the squashed cylinder by an ellipse with the minor and the major semi-axis R − 1, we approximate the shape of the squashed cylinder by an ellipse with the minor and the major semi-axis R − 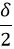 and R + and R + 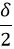 , respectively. Then, the curvatures to the first order in , respectively. Then, the curvatures to the first order in 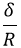 are are
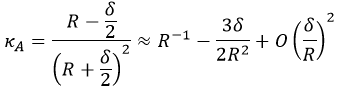 and
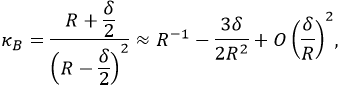 we obtain the following estimate 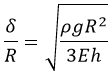 | (1) |
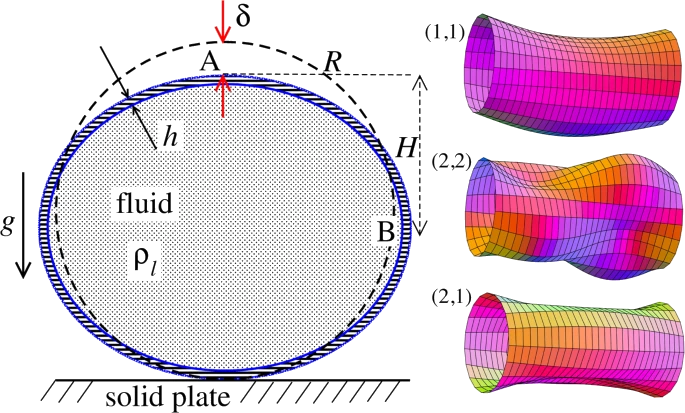
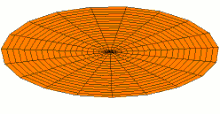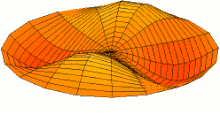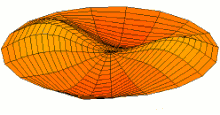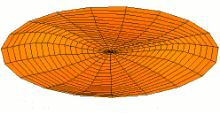
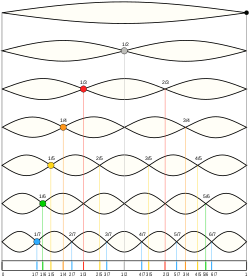
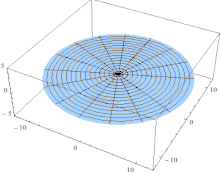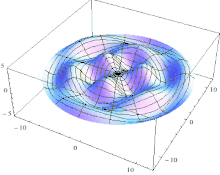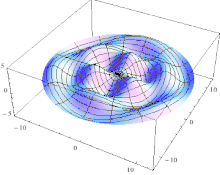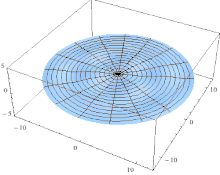
Schematic of the theoretical model for a vibrated earthworm represented as a liquid-filled elastic cylinder of length L with the Young’s modulus E, undeformed radius R, and shell thickness 5 h. The cylinder is filled with incompressible and inviscid fluid with the density ρl. Cross-section of the elastic cylinder deformed by the gravity in contact with a non-deformable solid plate. The dashed line shows the contour of an undeformed cylinder of radius R. The squashing depth is 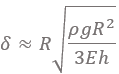 . Calculated spatial profiles of the first three lowest frequency vibration modes. The integer numbers in the parentheses denote, respectively, the number of the circumferential and the axial vibration mode. Viscoelastic properties of earthworms are poorly understood and previous works on mechanical properties of earthworms worm do not report the values of the Young’s modulus [57, 58]. However, mechanical properties of millimeter-sized nematode Caenorhabditis elegans worms have been recently reported [53], where a micropipette deflection setup [59] was used to study the stiffness of the worms. In particular, the effective bulk Young’s modulus of the worm body was found to be in the 105 … 106 Pa range, with the maximum value originating from the cuticle. On the other hand, it has also been suggested that all nematodes exhibit a universal elastic response dominated by the mechanics of pressurised internal organs [60]. Nevertheless, the values of the bulk modulus reported in [60] are of the same order of magnitude as those in [53]. Furthermore, the effective Young’s modulus of the cuticle strongly depends on its thickness [53, 60]. Thus, assuming that the elasticity of the worm body is entirely due to the stiffness of the cuticle, the Young’s modulus can reach 200 … 400 MPa [61]. Significantly, for the lowest expected value of the effective Young’s modulus of the cuticle E = 1 MPa [53, 60] the gravity squashing of the worm body remains small, as demonstrated below. We take the thickness of the cylindrical wall to be h = 50 μm, which corresponds to the combined thickness of the cuticle and the epidermis of earthworms [51]. Nevertheless, the values of the bulk modulus reported in [60]. The effective density of the internal body fluid can be estimated as ρl = 1100 kg/m3 because the body of the worm consists of a water-like liquid [48] and it also contains blood vessels filled with blood, where the density of blood plasma is approximately 1025 kg/m3 and the density of blood cells circulating in the system is approximately 1125 kg/m3. Finally, for the largest possible value of the worm radius used in our experiments R = 5 mm, we estimate the relative squashing from Eq to be 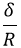 ≈ 4%. We note that in reality ≈ 4%. We note that in reality 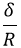 should be much smaller than 4% because the effective Young’s modulus of the cuticle could be about three orders of magnitude higher [61]. should be much smaller than 4% because the effective Young’s modulus of the cuticle could be about three orders of magnitude higher [61].
 Ivan S. Maksymov, Andrey Pototsky. Excitation of Faraday-like Body Waves in Vibrated Living Earthworms. Page 1 2 3 4 5 | George W. Hart. Mathematically Correct Breakfast
After being cut, the two halves can be moved but are still linked together, each passing through the hole of the other. 
If you visualize the key points and a smooth curve connecting them, you do not need to draw on the bagel. Here the two parts are pulled slightly apart. 
If your cut is neat, the two halves are congruent. They are of the same handedness.
You can toast them in a toaster oven while linked together, but move them around every minute or so, otherwise some parts will cook much more than others, as shown in this half. 
It is much more fun to put cream cheese on these bagels than on an ordinary bagel. In additional to
the intellectual stimulation, you get more cream cheese, because there is slightly more surface area.
Topology problem: Modify the cut so the cutting surface is a one-twist Mobius strip.
Calculus problem: What is the ratio of the surface area of this linked cut to the surface area of the usual planar bagel slice? Kyle Dropp, Joshua D. Kertzer and Thomas Zeitzoff. The less Americans know about Ukraine’s location, the more they want U.S. to intervene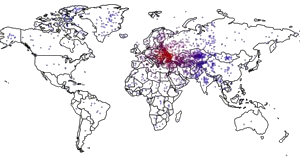
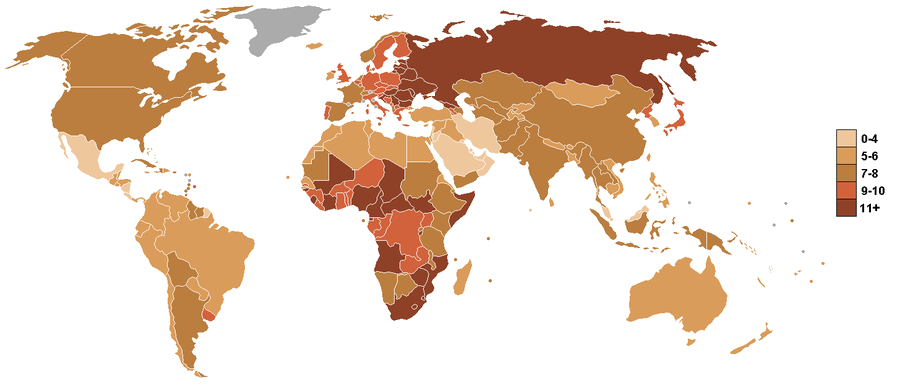
Since Russian troops first entered the Crimean peninsula in early March, a series of media polling outlets have asked Americans how they want the U.S. to respond to the ongoing situation. Although two-thirds of Americans have reported following the situation at least somewhat closely, most Americans actually know very little about events on the ground — or even where the ground is.
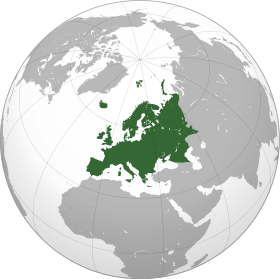
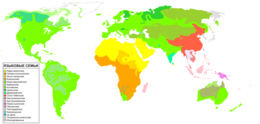
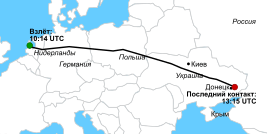
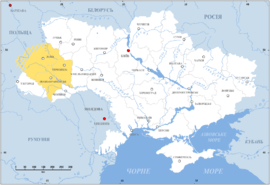
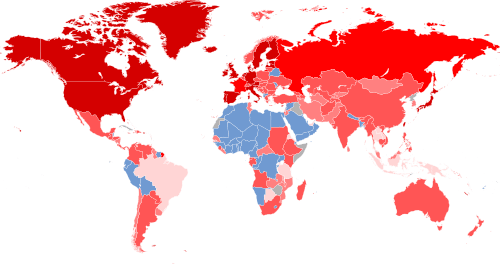
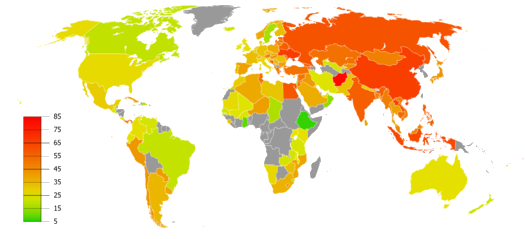
On March 28 — 31, 2014, we asked a national sample of 2,066 Americans, what action they wanted the U.S. to take in Ukraine, but with a twist: In addition to measuring standard demographic characteristics and general foreign policy attitudes, we also asked our survey respondents to locate Ukraine on a map as part of a larger, ongoing project to study foreign policy knowledge. We wanted to see where Americans think Ukraine is and to learn if this knowledge is related to their foreign policy views. We found that only one out of six Americans can find Ukraine on a map, and that this lack of knowledge is related to preferences: The farther their guesses were from Ukraine’s actual location, the more they wanted the U.S. to intervene with military force. Ukraine: Where is it? Survey respondents identified Ukraine by clicking on a high-resolution world map, shown above. We then created a distance metric by comparing the coordinates they provided with the actual location of Ukraine on the map. Other scholars, such as Markus Prior, have used pictures to measure visual knowledge, but unlike many of the traditional open-ended items political scientists use to measure knowledge, distance enables us to measure accuracy continuously: People who believe Ukraine is in Eastern Europe clearly are more informed than those who believe it is in Brazil or in the Indian Ocean.
About one in six Americans correctly located Ukraine, clicking somewhere within its borders. Most thought that Ukraine was located somewhere in Europe or Asia, but the median respondent was about 1,800 miles off — roughly the distance from Chicago to Los Angeles — locating Ukraine somewhere in an area bordered by Portugal on the west, Sudan on the south, Kazakhstan on the east, and Finland on the north. Anna Henschel. The Good, the Weird and the Hilarious Scientific Papers
On a day-to-day basis, postgraduate researchers are perusing hundreds of papers, preprints and journals. We set Google scholar alerts and experience an exhilarating cocktail of adrenaline and dopamine, when the daily digest of new articles arrives in our inbox. Did someone else get there first and publish the answer to the research question you have been working on? The fear ebbs away slowly, as you realize that yes, the paper is related to your field of research, but still not quite the same thing.
Next, you might file the newly acquired PDFs away, using your reference manager of choice. From 6+ years of using Mendeley, I have accumulated a mighty collection of knowledge in form of over a thousand academic papers. Among my collection of very serious scientific papers lives an odd folder called funny or interesting. Sometimes, I will come across an article that makes me laugh or is interesting, but doesn’t directly relate to anything I am working on. I started this folder in my undergraduate degree, when a lecturer asked us provocatively: So, have you heard of the dead salmon story?
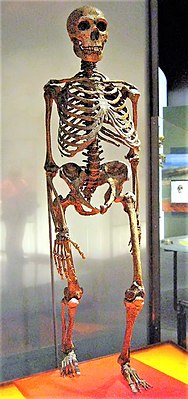
A dead salmon in the MRI scanner Neuroscientists and psychologists, bear with me for a moment while I let the rest of the postgraduate research community in on this strike of genius. Bennett and colleagues were scanning several inanimate objects in preparation of a new experiment, to check if their fMRI scanner worked as expected. Among these many inanimate objects, one was an Atlantic Salmon.
The authors ran their experimental task, set up for the following real study involving human participants. Thus, the dead fish was confronted with images of people engaging in social interactions. When the researchers later looked at the acquired data, they found something peculiar: a small cluster of significant brain activation. They wryly point out, that due to the “relatively small size of the salmon brain further discrimination between brain regions could not be completed. 
An Atlantic Salmon, the hero neuroscience needs. Picture taken from Wikipedia.
So, how is this possible? In their aptly titled poster Neural correlates of interspecies perspective taking in the post-mortem Atlantic Salmon: An argument for multiple comparisons correction, they describe a problem that is very common in fMRI research: neuroscientists conduct statistical tests on the many tiny parcels that the brain is partitioned in, so that a small proportion of random noise will turn out as ‘significant’ brain activation. To avoid this dead salmon effect, researchers have to control for the number of comparisons they make.
The ingenuity of this paper was rewarded with an Ig Nobel prize in 2012. The award is designed to highlight research, that first makes you laugh, and then makes you think. Only one laureate of the Ig Nobel went on to receive an actual Nobel prize so far: Sir Andre Geim. In one instance, he was able to levitate a frog using magnets, and in another, he was the first person to isolate graphene. Go figure, which prize he received for which achievement. Tweet, and you shall receive Curious, I turned to Twitter and asked if other users had favorite unusual studies. As it turns out, they had many. From marriage proposals hidden in acknowledgment sections, to thanking erupting volcanoes for forcing scientists to remain in Iceland and finish their paper, to a blank page entitled The unsuccessful self-treatment of a case of writer’s block. You can have a look at the thread yourself, as not all of the papers mentioned made it into this post.
A fantastic article that I came across through these Twitter recommendations was published in the British Medical Journal’s Christmas edition. In this randomized-controlled trial the authors set out to investigate how effective a parachute is when jumping out of an aircraft, compared to jumping with an empty backpack. The researchers describe the process of their participant recruitment as follows: |
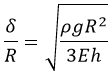

![]() ≈ 4%. We note that in reality
≈ 4%. We note that in reality ![]() should be much smaller than 4% because the effective Young’s modulus of the cuticle could be about three orders of magnitude higher [61].
should be much smaller than 4% because the effective Young’s modulus of the cuticle could be about three orders of magnitude higher [61].![]()