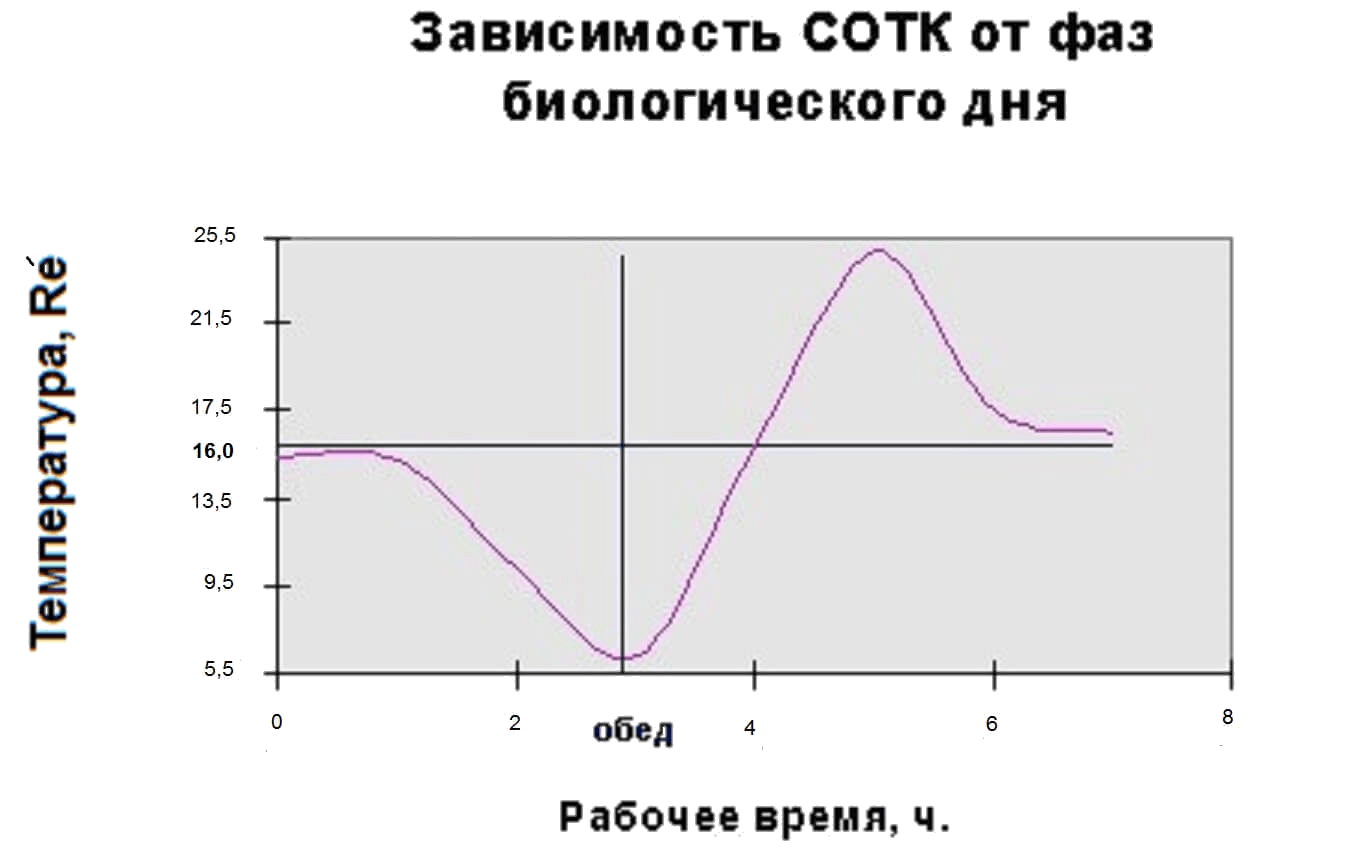
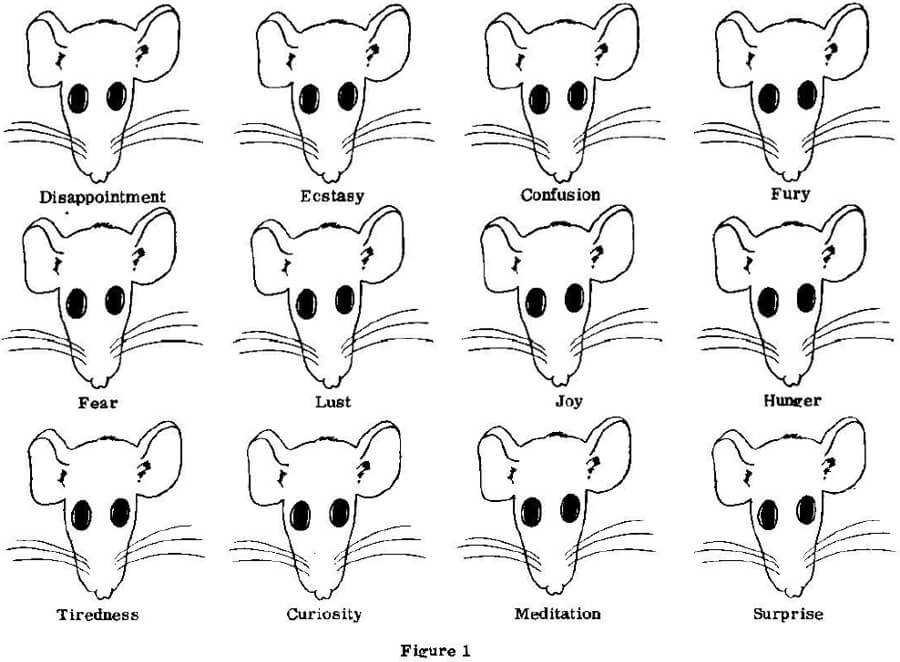
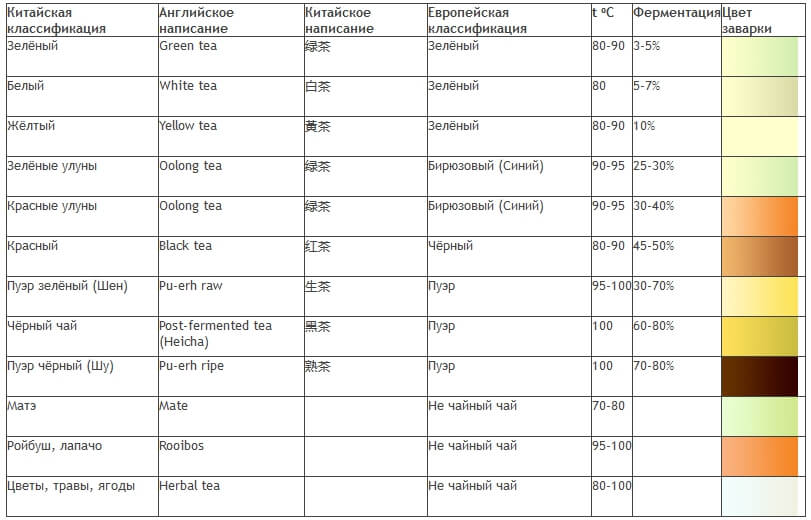
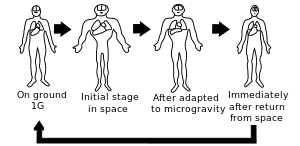
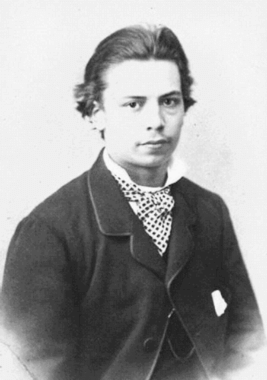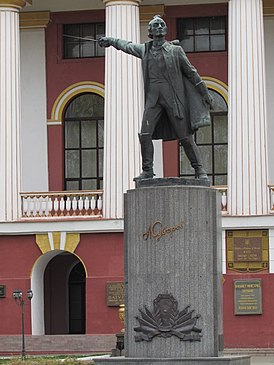 Т.Е. Нефедова, Л.И. Войтюк, А.Е. ПрилуцкийУДК 187.13.15.05 Данная работа посвящена исследованию проблем субъективного ощущения термальной комфортности. Актуальность исследования сезонной динамики СОТК в рамках биологического дня возросла в последнее время в связи с очевидным влиянием СОТК на интенсивность и отдачу труда как физического, так и интеллектуального. В литературе имеется значительное количество данных и рекомендаций по вопросам интенсификации труда, однако проблема СОТК практически не обсуждается, что, с нашей точки зрения, является существенным упущением. Для внесения ясности в этот важный вопрос нами были проведены эксперименты с целью объективной фиксации динамики СОТК и создания статистически полной феноменологии этого явления. С использованием этой методики был получен представительный массив данных, обработка которого методами корреляционного анализа с использованием математического обеспечения, разработанного на ЭВМ ЕС 1057, привела нас к выводу о существенной симбатности динамик квазистационарной температуры ареала и СОТК. Обнаружена явная субъективная гипертермия в области времен, лежащей в малой окрестности точки, которой мы дали условное наименование обед. Наличие такой закономерности позволяет разработать определенные рекомендации по интенсификации труда и повышению его производительности. Мы, в частности, предлагаем отойти от общепринятой схемы рабочего дня: и заменить ее на более сложную структуру, включающую переходные режимы: В конкретном случае может оказаться, что последняя фаза данной схемы может лежать вне области времен, отводимой в качестве рабочего времени в соответствии с регламентацией закона. В этом случае мы предлагаем следующий вариант схемы: Были проведены испытания предложенных схем, и хотя эксплуатационный опыт еще невелик, мы пришли к выводу о целесообразности их дальнейшего использования, т.к. они являются, на наш взгляд, многообещающими в плане интенсификации труда и повышения его производительности. Вышесказанное позволяет сделать следующие выводы.
13 Jan 84 Текст публикуется по ТЧК |  Экспонаты Омар Хайям
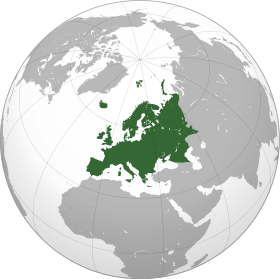
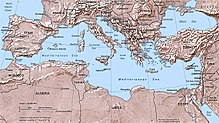
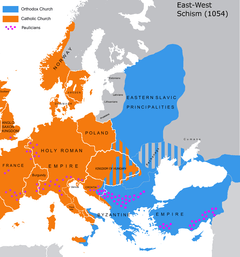
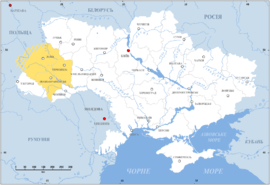
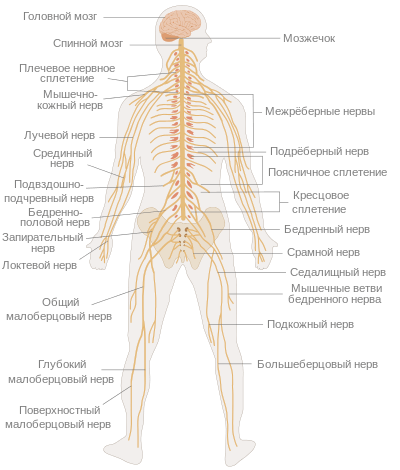
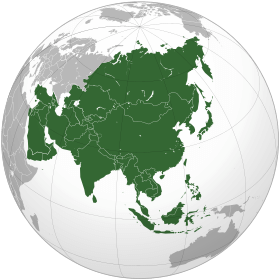
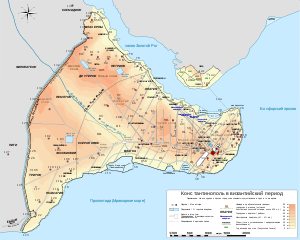
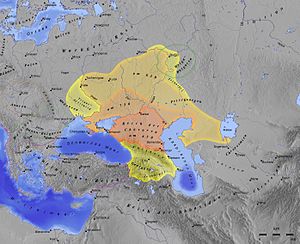
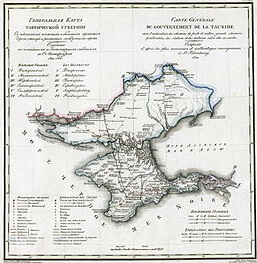
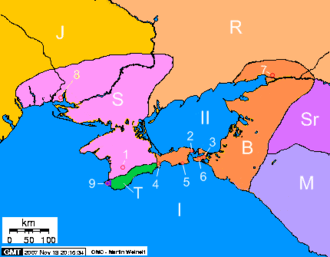
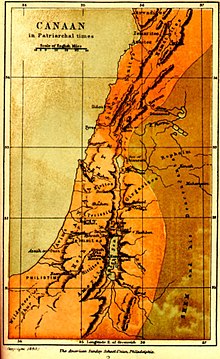
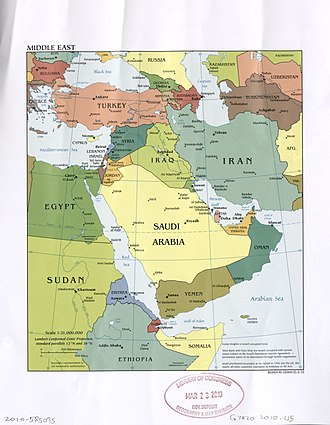
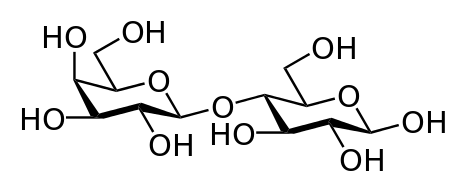
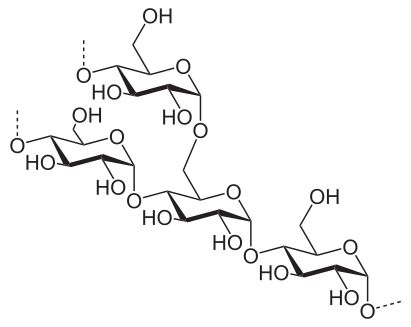
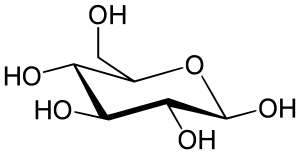
Родиной Омара Хайяма был Хорасан — область, расположенная к востоку и юго-востоку от Каспийского моря. В настоящее время большая часть Хорасана с городами Мешхед и Нишапур является одноименной провинцией Ирана, северная часть с городами Ашхабад и Мары составляет основную часть Туркменистана, а восточная часть с городами Герат и Балх входит в состав Афганистана. Учился Хайям в Нишапуре, а затем в крупнейших центрах науки того времени, в Балхе и Самарканде, где написал трактат О доказательствах задач алгебры и алмукабалы. На богатом историческом материале исследователи доказали заслуги Омара Хайяма как ученого, который сделал ряд важнейших открытий в области астрономии, математики и физики. С 1074 года Хайям возглавлял крупнейшую астрономическую обсерваторию. В середине 90-х XI века совершил паломничество в Мекку. Последние годы жизни Хайям провел в Нишапуре. Список математических трактатов Омара Хайяма Трудности арифметики — Местонахождение рукописи не найдено; Алгебраический трактат без названия — Тегеран; Трактат о доказательствах задач алгебры и алмукабалы — Париж, Лейден, Лондон, Нью-Йорк, Рим; Комментарии к трудностям во введениях книги Евклида — Лейден. Известные нам математические результаты Хайяма относятся к трем направлениям: к алгебре, к теории параллельных, к теории отношений и учению о числе. Во всех этих направлениях Хайям имел в странах ислама выдающихся предшественников и преемников. Во многом он отправлялся от классиков греческой и эллинистической науки — Аристотеля, Евклида, и др., но вместе с тем он выступает как яркий представитель новой математики с ее мощной и определяющей вычислительно-алгоритмической компонентой. Здесь мы дадим краткую характеристику математического творчества Хайяма, отсылая за подробностями к нашим комментариям к переводам его трактатов. Начнем с алгебры. Алгебраический трактат Хайяма можно разбить по порядку на пять разделов: 1) введение, 2) решение уравнений 1-й и 2-й степени, 3) решение уравнений 3-й степени, 4) сведение к предыдущим видам уравнений, содержащих величину, обратную неизвестной, 5) дополнение. Во введении мы впервые находим определение предмета и метода алгебры.
Таким образом, предмет алгебры — это неизвестная величина, дискретная или же непрерывная. Неизвестные и данные величины могут быть и отвлеченными отношениями. Отнесение неизвестных величин к известным есть составление уравнения. Немного далее Хайям говорит:   |
Дорогой Редакции
, where α and q are parameters.
.
