|  Омар ХайямОкончание. На предыдущую. К началу. Третья книга Комментариев посвящена учению о составлении отношений, недостаточно развитому у Евклида. Это учение представляло для математиков стран ислама особую важность в связи с приложениями к теории музыки и, главное, тригонометрии. Это совершенно понятно, если учесть, что составление отношений соответствует умножению чисел. Незадолго до Омара Хайяма аль-Бируни обосновал при помощи составных отношений практические правила индийцев — так называемые епные правила. В этой книге Хайям отходит от Аристотеля в учении о числе. Признавая вслед за многими древними, что число в собственном смысле это натуральное число, собрание единиц, Хайям предлагает ввести более широкое абстрактное понятие о числе, как о действительном положительном числе. За Хайямом в теории отношений и учении о числе последовал Насир ад-Дин ат-Туси. В Европе единое понятие действительного числа появляется в конце XVI в. у С. Стевина. Критике теории отношений V книги Начал с позиций вычислительной математики посвящен целый ряд трудов математиков XVII в.; основную роль в разработке идеи действительного числа сыграли Р. Декарт и И. Ньютон, определивший число как отвлеченное отношение произвольной величины к единичной величине того же рода. Впрочем, строгие теории действительного числа появились только в конце XIX в. Таким образом, работы математиков стран ислама, и среди них работа Омара Хайяма, являются существенными звеньями в цепи исследований, приведших к строгой теории действительного числа и основанному на ней математическому анализу. Фалес Милетский Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и, вообще, первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России. Фалесу Милетскому приписывают простой способ определения высоты пирамиды. В солнечный день он поставил свой посох там, где оканчивалась тень от пирамиды. Затем он показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха. Пифагор Самосский Его отцом был некий Мнесарх из Самоса, человек благородного происхождения и образования. Спасаясь от тирании Поликрата, Пифагор ок. 530 до н.э. покинул Самос. Историю его жизни трудно отделить от легенд, представляющих Пифагора в качестве полубога и чудотворца, совершенного мудреца и великого посвященного во все тайные доктрины греков и варваров. По преданию, Пифагор объездил весь свет и собрал свою философию из различных систем, к которым имел доступ. Так, он изучал эзотерические науки у брахманов Индии, астрономию и астрологию в Халдее и Египте. В Индии он и по сей день известен под именем Яваначарья. По возвращении он поселился в Кротоне, в Южной Италии, где проповедовал свое учение многочисленным последователям, часть которых образовала своего рода религиозный орден, или братство «посвящённых». Этот орден фактически пришел в Кротоне к власти, однако из-за антипифагорейских настроений в конце 6 в. до н.э. Пифагору пришлось удалиться в Метапонт, где он и умер в 500 до н.э. Пифагор стоял у истока греческой науки, был вынужден заниматься всем сразу: арифметикой и геометрией, астрономией и музыкой. Его целью было разобраться в строении Вселенной и человеческого общества. Он первый заметил, что сила и единство науки основаны на работе с ИДЕАЛЬНЫМИ ОБЪЕКТАМИ. Например, прямая линия — это не тетива натянутого лука и не луч света: ведь они имеют небольшую толщину, а линия толщины не имеет. Несовершенные природные тела являются лишь грубоватым подобием идеальных математических сущностей. Первая научная модель мира, предложенная Пифагором — все природные тела и процессы суть искаженные подобия идеальных тел и движений — а закономерности идеальных объектов выражаются с помощью чисел.
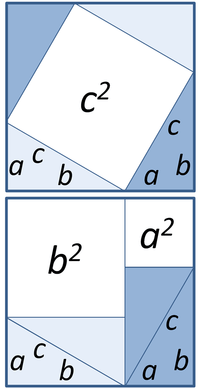
Пифагоровы числа — комбинация из трех целых чисел, удовлетворяющих соотношению Пифагора: x2 + y2 = z2. Например, тройка чисел: 32 + 42 = 52. Пифагоровы штаны — шуточное название теоремы Пифагора, возникшее в силу того, что раньше в школьных учебниках эта теорема доказывалась через доказательство равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата, построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали школьникам покрой мужских штанов, что породило следующее стихотворение: Пифагоровы штаны — на все стороны равны… Евклид О Евклиде почти ничего неизвестно, откуда он был родом, где и у кого учился. Все же у нас нет оснований сомневаться в существовании Евклида, тем более что в этом не сомневались и позднейшие греческие ученые, кое-что рассказывавшие о нем. Папп Александрийский сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Как-то царь Птолемей I спросил Евклида, нет ли более короткого пути для изучения геометрии, чем штудирование Начал. На это Евклид смело ответил, что
Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: Феномены, Оптика и Сечение канона. Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором Начал, по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание Начал далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения Начал, как на нечто окончательно установленное.  Фрагмент старейшего папируса с диаграммами из «Элементы геометрии» Евклида Эратосфен Киренский Родился в Кирене. Образование получил в Александрии, а затем в Афинах у известных наставников, поэта Каллимаха, грамматика Лисания, а также философов — стоика Аристона и платоника Аркесилая. Вероятно, именно благодаря столь широкому образованию и разнообразию интересов ок. 245 до н.э. Эратосфен получил от Птолемея III Эвергета приглашение вернуться в Александрию, чтобы стать воспитателем наследника престола и возглавить Александрийскую библиотеку. Эратосфен принял это предложение и занимал должность библиотекаря вплоть до своей кончины. Один из самых разносторонних ученых античности. Особенно прославили Эратосфена труды по астрономии, географии и математике, однако он успешно трудился и в области филологии, поэзии, музыки и философии, за что современники дали ему прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. второй, по-видимому, также не содержит ничего уничижительного: им желали показать, что во всех науках Эратосфен достигает не высшего, но превосходного результата. Его научные таланты удостоились высокой оценки современника Эратосфена, Архимеда, который посвятил ему свою книгу Эфодик. Сочинения Эратосфена не сохранились, мы имеем от них лишь фрагменты. Трактаты Эратосфена Удвоение куба и О среднем были посвящены решению геометрических и арифметических задач, в Платонике он обращается к математическим и музыкальным основам платоновской философии. Самым знаменитым математическим открытием Эратосфена стало т.н. решето Эратосфена, с помощью которого находятся простые числа. Эратосфен является основоположником научной географии. В его Географии в 3 книгах содержалась история географических открытий, а также рассматривался ряд физических и математических проблем, связанных с географией, включая указание на сферическую форму Земли и описание ее поверхности. Однако самым известным достижением Эратосфена в области географии был изобретенный им способ измерения размеров Земли, изложению которого посвящен трактат Об измерении Земли. Метод основывался на одновременном измерении высоты Солнца в Сиене и в Александрии, лежащих примерно на одном меридиане, в момент летнего солнцестояния. И хотя остается спорным, получилось ли у Эратосфена в итоге 250000 стадий или 252000, в любом случае этот результат замечателен — диаметр Земли оказался всего лишь на 80 км меньше, чем фактический полярный диаметр. В этой же работе были рассмотрены и астрономические задачи, такие, как оценка размера Солнца и Луны и расстояния до них, солнечные и лунные затмения и продолжительность дня в зависимости от географической широты. 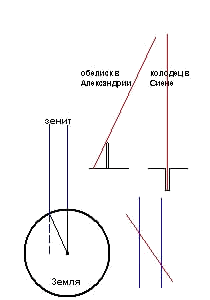 Эратосфена можно считать также основателем научной хронологии. В своих Хронографиях он пытался установить даты, связанные с политической и литературной историей Древней Греции, составил список победителей Олимпийских игр. В трактате О древней комедии, где анализировались произведения афинских драматургов, Эратосфен выступил как литературный критик и филолог. Эратосфен написал также поэму Гермес, повествующую о рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий эпос, Гесиод, посвящен смерти поэта и каре, постигшей его убийц. Эратосфен написал также трактат Катастеризмы — описание созвездий и изложение посвященных им мифов. Эратосфену принадлежал еще ряд работ по истории и философии, которые не сохранились. Герон Александрийский
Время его жизни неопределенно, известно только, что он цитировал Архимеда, его же самого цитировал Папп. Герон несколько старше Птолемея Менелая. В его Сферике содержится геометрия сферы и рассматриваются сферические треугольники — предмет, которого нет у Евклида. Здесь мы находим теорему Менелая для треугольника в обобщенном для сферы виде. В астрономии Птолемея немало вычислений в шестидесятичных дробях, а трактат Менелая геометричен строго в духе евклидовой традиции. Сам Герон описал лунное затмение 62. В настоящее время преобладает мнение, что он жил в I в. н.э. Занимался геометрией, механикой, гидростатикой, оптикой; изобрел прототип паровой машины и точные нивелировочные инструменты. Наибольшей популярностью пользовались такие автоматы Герона, как автоматизированный театр, фонтаны и др. Герон описал диоптр — прибор для измерения углов — прототипа современного теодолита, опираясь на законы статики и кинетики, привел описание рычага, блока, винта, военных машин. В оптике сформулировал законы отражения света, в математике — способы измерения важнейших геометрических фигур. Основные произведения Герона — это Иетрика, Пневматика, Автоматопоэтика, Механика, Катоптика и др. Герон использовал достижения своих предшественников: Евклида, Архимеда, Стратона из Лампсака. Его стиль простой и ясный, хотя порой бывает чересчур лаконичен или нестроен. Интерес к сочинениям Герона возник в III в. н. э. Греческие, а затем византийские и арабские ученики комментировали и переводили его произведения. Математические работы Герона являются энциклопедией античной прикладной математики. Работы его дошли до нас не полностью. Из его работ известны Механика, Книга о подъемных механизмах, Пневматика, Книга о военных машинах, Театр автоматов, Метрика. В лучшей из них — Метрике даны определение шарового сегмента, тора, правила и формулы для точного и приближенного вычисления площадей правильных многоугольников, объемов усеченных конуса и пирамиды, приводится так называемая формула Герона для определения площади треугольника по трем сторонам, встречающаяся у Архимеда; даются правила численного решения квадратных уравнений и приближенного извлечения квадратных и кубических корней. В Метрике исследуются простейшие подъемные приспособления — рычаг, блок, клин, наклонная плоскость и винт, а также некоторые их комбинации. При исследовании Простых машин пользуется понятием момента. Учитывал силу трения и рекомендовал при работе со сложными механизмами несколько увеличивать силы, прилагаемые к ним. В Пневматике им рассмотрен ряд остроумных гидропневматических приборов. В Театре автоматов описал храмовые и театральные автоматы своего времени. У Герона встречается соотношение Ц2 ≫ 17/12, где 17/12 как известно, является четвертой подходящей дробью к Ц2. Содержание математических трудов Герона догматично, правила чаще всего не выводятся, а поясняются на примерах. Это сближает труды Герона с работами математиков Древнего Египта и Вавилона. В 1814 году было найдено сочинение Герона О диоптре, в котором изложены правила земельной съемки, фактически основанные на использовании прямоугольных координат. Герон писал основные достижения античного мира в области прикладной механики. Он изобрел ряд приборов и автоматов, в частности прибор для измерения протяженности дорог, действовавший по тому же принципу, что и современные таксометры, автомат для продажи священной воды, различные водяные часы и другое. Влияние работ Герона можно проследить в Европе вплоть до эпохи Возрождения. Диофант
Диофант — древнегреческий математик из Александрии. Мы очень мало знаем о нем. В одной из эпиграмм Палатинской антологии говорится:
Отсюда нетрудно подсчитать, что Диофант прожил 84 года. Однако, для этого вовсе не нужно владеть мудрым искусством его. достаточно уметь решать уравнение первой степени с одним неизвестным, а это умели делать египетские писцы еще в 18 в. до н.э. Но когда же жил Диофант? Теон александрийский в своих комментариях к Альмагесту Прометея привел отрывок из сочинений Диофанта. Поскольку деятельность Теона падает на вторую половину IV века нашей эры, очевидно, Диофант не мог жить позднее середины IV века. Этим определяется верхний предел промежутка возможного времени жизни Диофанта. С другой стороны, сам Диофант в своей работе О многоугольных числах дважды упоминает Гипсикла, математика, жившего в Александрии в середине II в. до н.э. Итак, нижним пределом является вторая половина II в. до н.э. Таким образом, получаем промежуток в 500 лет! Сузить этот промежуток попытался П. Таннери, известный, историк науки, издатель критически проанализированного текста сочинений Диофанта, который теперь принят в качестве канонического. В библиотеке Эскуриала он нашел отрывок из письма Михаила Пселла, византийского ученого XI в., текст которого был искажен при переписках. После восстановления Таннери один из отрывков письмо может быть переведен так:
Известно, что Анатолий Александрийский составил Введение в арифметику в 10 частях, фрагменты из которого дошли до нас в передаче Ямблика. но Анатолий, познания которого в арифметике, геометрии и астрономии превозносит Евсевий, жил в Александрии в середине III в., причем в 270 покинул ее, став епископом Лаодинийским. Таким образом, если Таннери правильно прочел письмо Пселла, то Диофант жил в середине III в. н.э. Это подтверждается еще и тем обстоятельством, что сама Арифметика посвящена достопочтеннейшему Дионисию, который, как это видно из введения к первой книге, интересовался наукой о числах и ее преподаванием. Между тем с 231 по 247 во главе Александрийского христианского училища для юношества стоял Дионисий, ставший в 247 епископом Александрии. По предположению Таннери именно ему и была посвящена Арифметика. Поэтому обычно теперь считают, что Диофант жил около 250 года. Диофант автор трактата Арифметика в 13 книгах, посвященных главным образом исследованию неопределенных уравнений. ал-Хорезми
Имя Ал-Хорезми Мухаммед бен-Муса Хорезми Мухаммед бен Мусса указывает на его родину — среднеазиатское государство Хорезм, бен Муса — значит сын Мусы, а одно из прозвищ ученого — ал-Маджуси — говорит о его происхождении из рода магов по-арабски маджусь. Ариабата
Индийский астроном и математик. Родился в Кусумапуре. В Паталипутре преподавал тригонометрию и алгебру. Из написанных им сочинений сохранилось только одно — Ариабхатия, в котором в стихотворной форме изложены математические сведения, необходимые для астрономических вычислений; приведены задачи на составление и решение уравнений, извлечение квадратного и кубического корней и др. Большая часть этой работы посвящена астрономии и сферической тригонометрии. Приведены также 33 правила по арифметике, алгебре и тригонометрии на плоскости. Продемонстрировано исследование неопределенных уравнений с помощью бесконечных дробей. Является автором ещё пяти трудов по математике, измерению времени, небесной сфере и др. Ариабхата изобрёл понятие нуля, нашел весьма точное значение числа π и ввел в тригонометрию функцию, высказал догадку, что вращение небес — только кажущееся и является следствием вращения Земли вокруг своей оси. Древнейшие дошедшие до нас индусские тексты свидетельствуют о том, что у индийцев были глубокие познания в области астрономии. Эти знания частично были усвоены и перенесены в западный мир посвященными или адептами звездной науки. Фалес, Пифагор, Платон и другие философы, путешествуя по Востоку, приносили на землю эллинов глубокие сокровенные истины. По прошествии веков эти идеи, обогащенные опытом античности, снова пришли на индийскую землю. Влияние прославленной Александрийской школы сказалось на воззрениях индусских ученых о мире звезд. Ариабхатиа переводе означает Учение Ариабхаты — в нем изложены математические сведения, необходимые для астрономических вычислений, встречаются задачи на составление и решение уравнений, суммирование кубов натуральных чисел, извлечение квадратного и кубического корней и др. В своем труде Ариабхата высказал догадку, что вращение небес — только кажущееся.  Трактат Сурья-сиддханты — Солнечной доктрины делится на 14 глав и составлен в стихах. В первых разделах говорится о подразделениях времени и основных частях года. Много места уделено движению Солнца по эклиптике. Попутно с представлениями о движении светил приводятся и данные об употребляемых астрономических инструментах. Существенной данью традиционным космогоническим представлениям индийцев явилось в этой работе учение о четырех югах. Более научным разделом Солнечной доктрины являются главы о движении планет: греко-римские открытия полностью усваиваются здесь индийцами, и планетарная символика становится с этих пор частым явлением в художественной литературе. Повторяя многие положения Сурья-сиддханты Ариабата идет дальше — обгоняет в своих выводах не только индийских, но и западных астрономов. Текст публикуется по Галерея великих математиков |