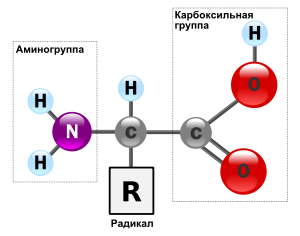
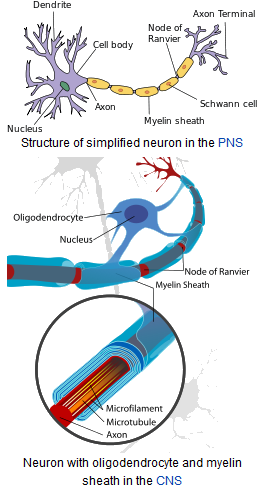
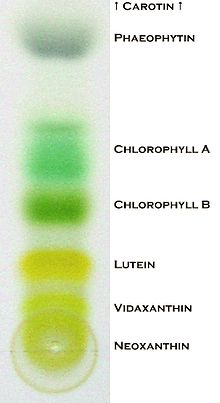
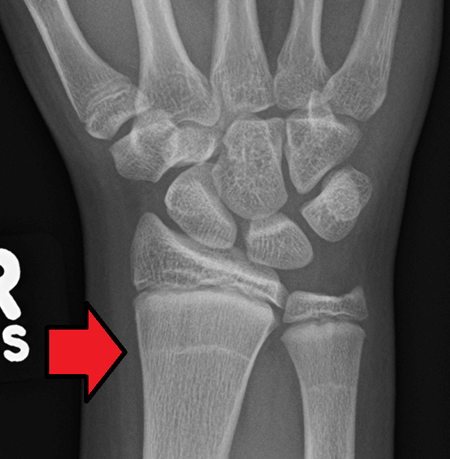
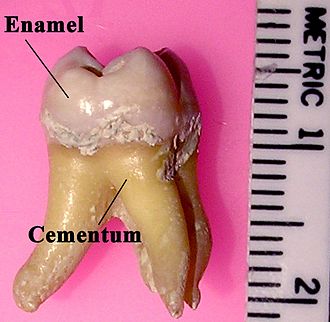
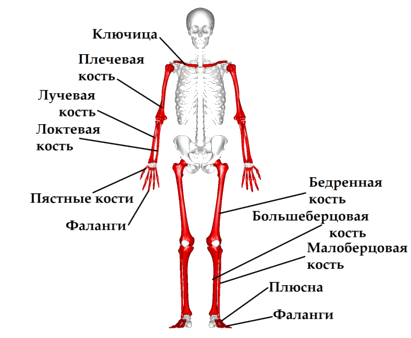
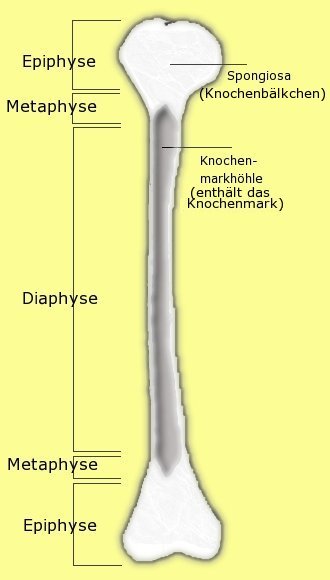
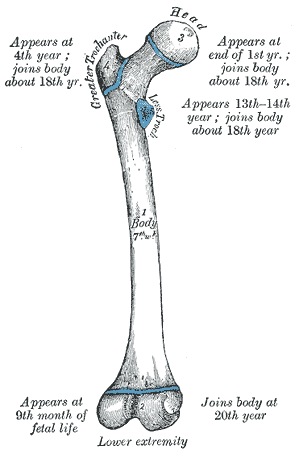
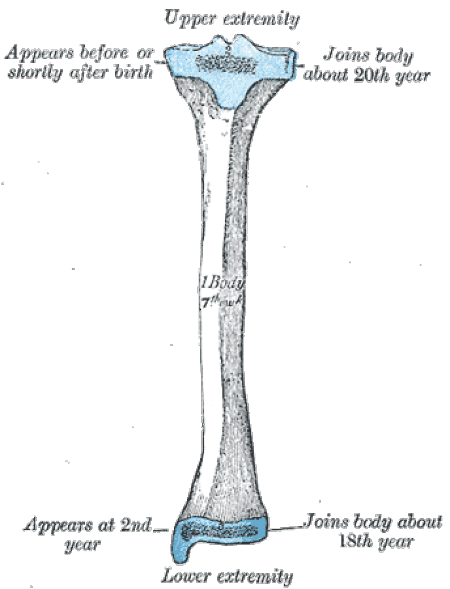
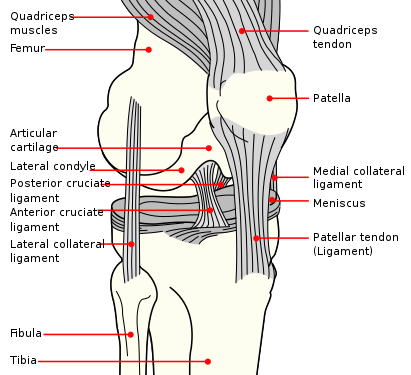
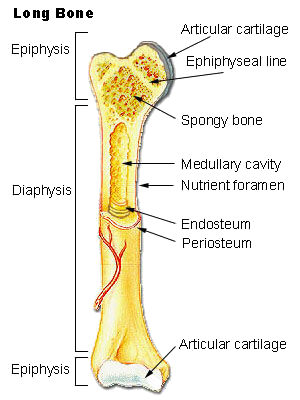
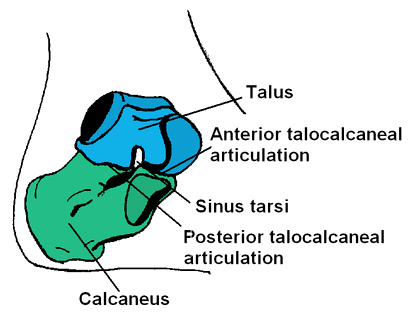
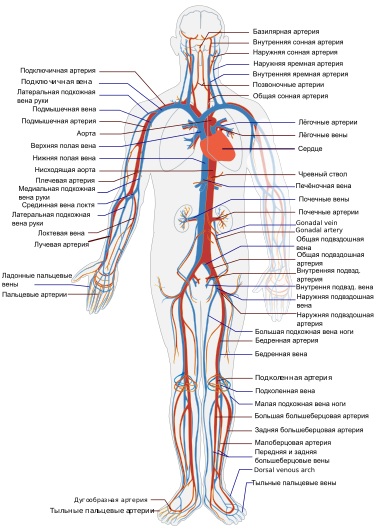
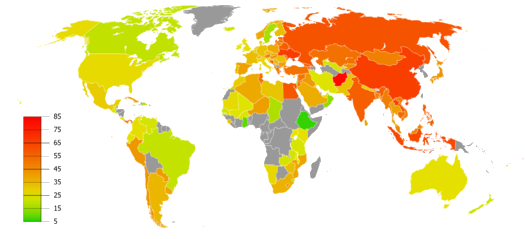
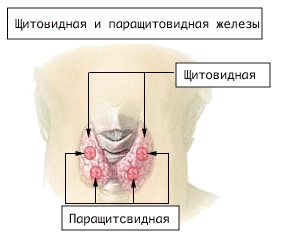
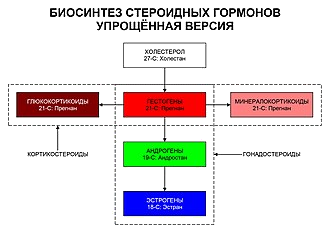
Л.И. Ярмолинский Л.И. Ярмолинский
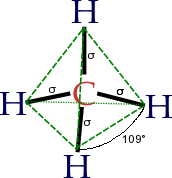
УДК 194.46.94/28-18 Проблема, рассматриваемая в предлагаемой работе, имеет весьма долгую предысторию. Достаточно вспомнить широко известную формулу делать из мухи слона,что, несомненно, представляет собой цитату из какого-то древнего трактата по мускэлефологии. Однако до настоящего времени не проводились достаточно серьезные исследования динамики трансформации в системе муха — слон несмотря на то, что она издавна используется при проведении научных исследований, так и в промышленности. Автор считает, что настало время применить современный научный подход к изучению ТМС для объяснения известных эмпирических закономерностей, а также для построения единой ТМС-теории. Первым этапом предлагаемого исследования был функциональный анализ трансформируемой пары. В результате выявлено: - Для обоих объектов характерно инертное связующее звено.
- Хобот слона и хоботок мухи функционально эквивалентны.
- Слоновьи уши есть, несомненно, изачаточные мушиные крылья.
- При ТМС задняя пара лапок мухи, очевидно, трансформируется в хвост слона.
Таким образом, можно сделать вывод, что объекты пары муха — слон функционально эквивалентны. Использование указанных закономерностей делает возможным исследование термодинамики ТМС. Выявлено, что количество слонов в произвольно фиксированной местности прямо пропорционально среднегодовой температуре. Следует отметить, правда, что одновременно растет и количество мух. Однако в целом можно предположить, что формула ТМС имеет вид: M + Q = CНиже приведено доказательство этого факта, основанное на известных теоретических результатах. Масса и энергия связаны выражением E = mc2Если обозначить массу покоя мухи mм, а слона — mс, получаем: E0 + mмc2 = mсc2Т.к. mм ≪ mс, то выражение преобразуется следующим образом: mсc2 = mмc2 + (mсc — mм)c2.Следует предположить, что превращение в системе муха — слон идет через нестабильные промежуточные формы. Поэтому обнаружить мухослона или слономуху практически невозможно. Таким образом, теоретическое обоснование получили следующие эмпирические законы. - Превращения в системе муха — слон требует значительных энергетических или материальных затрат.
- Слоны встречаются преимущественно в жарких странах.
В свете рассматриваемых вопросов считаю необходимым обратить внимание также на проблему вымирания мамонтов. Очевидно, что в условиях низких температур равновесие в системе муха — слон должно быть смещено в сторону муха. Но если предположить, что возникавшие мамонты фиксировались за счет быстрого понижения температуры, а затем изымались из среды первобытными охотниками или вмораживались в вечную мерзлоту, то сохранение некоторого количества формы слон становится вероятным. Позднее, ввиду прекращения резких похолоданий, исчезли условия фиксации слонов, что выглядело как вымирание мамонтов. Подавляющее большинство находок мамонтов связаны либо с кухонными отбросами человека, либо с вмораживанием в вечную мерзлоту. В заключение автор выражает надежду, что мускэлефология, переживающая ныне второе рождение, будет развиваться как динамичная многопроблемная наука. Перечислим только некоторые из основных направлений:
✓ исследование трансформации в системах слон — муха — мамонт и слон — мамонт, минуя стадию муха;
✓ изучение причин несоответствия видового разнообразия слонов и мух;
✓ возможность реализации ТМС с использованием дешевых источников энергии.
Текст публикуется по ТЧК |  ал-Хорезми Ал-Хваризми родился в Средней Азии, г.Хива, территория современного Узбекистана. Сведений о жизни и деятельности ал-Хорезми, к сожалению, почти не сохранилось. Известно лишь, что он возглавлял в Багдаде библиотеку Дома мудрости, своего рода Багдадской академии, при халифе ал-Мамуне. А при другом халифе ал-Васике, преемнике ал-Мамуна, он возглавлял экспедицию к хазарам.
В 975 — 997 он написал Ключ к Наукам, первая арабская энциклопедия знаний, которая была организована на научных принципах. Ее содержание было классифицировано:
✓ местные знания — юриспруденция, схоластическая философия, грамматика, секретарские обязанности, просодия и поэтическое искусство, история;
✓ иностранные знания — философия, логика, медицина, арифметика, геометрия, астрономия, музыка, механика, алхимия.
Как ученый Ал-Хваризми становится известным из его достижений в математике. Его работа над арифметикой была переведена на латынь в XII столетии, и хотя оригинал потерян, латинский перевод Ал-Хваризми об индийских числах все еще существует. Его название давало начало математическому термину арифметика.
Другая работа Ал-Хваризми, Книга Интеграции и Уравнения, буквально сокращение и сравнение, был синтез индийской алгебры и греческой геометрии и имел самый глубокий эффект на развитие науки. Латинские переводы, резюме и комментарии были написаны в XII столетии. Математический термин алгебра был получен из ее названия. 
Ал-Хваризми также издал астрономические и тригонометрические таблицы, базируемые главным образом на арабском переводе индийской астрономической работы Brahma-siddhanta, которая была написана приблизительно за 100 лет до этого. В течение 10-ого столетия Maslama al-Majrti пересмотрел таблицы и добавил его собственный таблицы тангенса, Ал-Хваризми добавил табулирование функции синуса. В той версии таблицы были переведены на латинский в 1126 Adelard of Bath.
Имя ал-Хорезми в видоизмененной форме Algorithmus превратилось в нарицательное слово алгоритм и сначала означало всю систему десятичной позиционной арифметики. Впоследствии этот термин приобрел более широкий смысл в математике как правило выполнения операций в определенном порядке. Вспомним, к примеру, алгоритм Евклида или алгоритм решения квадратного уравнения.  К перечню экспонатов галереи Пьер Ферма
Пьер Ферма родился в Beaumont-de-Lomagne. Его отец, Доминик Ферма, был зажиточным торговцем, вторым городским консулом; мать — преподавательница математики. Пьер Ферма получил домашнее образование. Обучался праву сначала в Тулузе, а затем в Бордо и Орлеане. Получил профессию юриста. В 1631 он выкупил должность королевского советника парламента в Тулузе. Быстрый служебный рост позволяет ему стать членом Chambre de l’edit в Castres в 1648. Именно этой должности он обязан добавлением к своему имени указателя знатности — частицы de; с этого времени он становится Пьером де Ферма.  В математике Пьер Ферма становится одним из создателей аналитической геометрии и теории чисел, автор работ в области теории вероятностей, оптики, исчислении бесконечно малых величин. Теорема была сформулирована им в 1637 году, на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы привести его на полях. |