Ivan S. Maksymov, Andrey Pototsky

Then, we neglect viscoelastic damping and obtain a linear model of parametrically excited subharmonic body waves in an elastic fluid-filled cylinder. We follow the approach developed for subharmonic vibrations of a water drop placed on an oscillating solid plate [30], where natural vibration frequencies of a cylinder squashed by gravity are considered Fig. 5. The degree of squashing is characterised by the indentation depth δ that, in turn, is proportional to the gravity acceleration g. In the co-moving frame of the vibrating plate, the gravity is time-dependent. This means that the effect of the vibration is equivalent to periodically varying the squashing of the cylinder. Therefore, in the linear regime, natural frequencies of the squashed cylinder are periodically modulated, thereby leading to a parametric type of forcing.

To the best of our knowledge, the analysis of the vibrational frequencies of a cylinder supported by a solid plate along its entire length has not been reported. Therefore, we estimate the order of magnitude of the natural frequencies by using the well-known result for a cylinder with freely supported ends [62, 63, 64], as demonstrated below. A comprehensive review of the linear and nonlinear vibration and instabilities of cylindrical shells and plates can be found in [47, 65, 66].

In cylindrical coordinates, the axial u(r, θ), azimuthal v and radial w displacements of the shell of a cylinder with freely supported ends can be written as

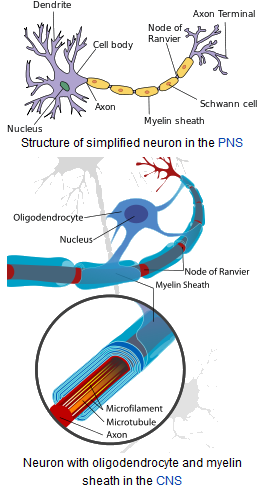
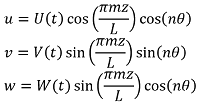(2)

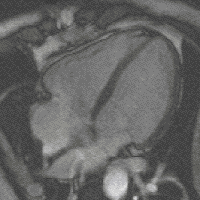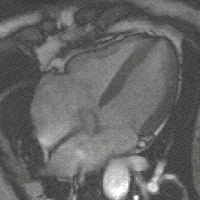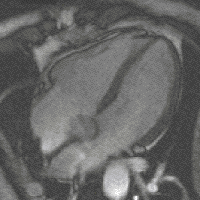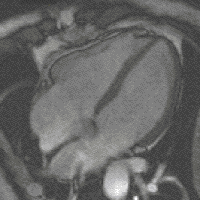
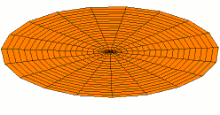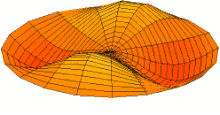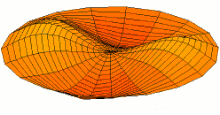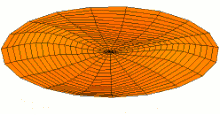
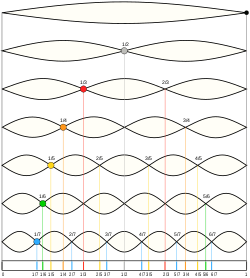
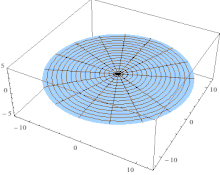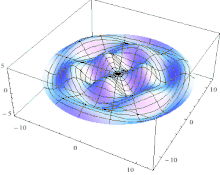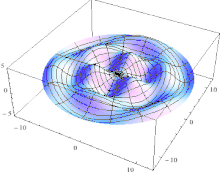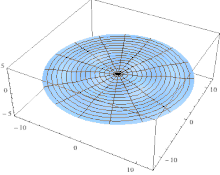
where the integers n and m determine the circumferential and the axial vibration modes, respectively. As a representative example, in Fig. 5 we show the first three lowest frequency modes.

For 1, the deviation of vibrational frequencies from those of a circular cylinder is of first order in [67]. This allows us to write the equations of motion for the amplitudes U, V, W as

(3)

where x = (U, V, W), J₀ is the Jacobian matrix corresponding to the circular cylinder and J₁ is its first order correction due to squashing. When the solid plate is vibrated with the frequency ω, its vertical displacement is given by Acos(ωt), where A is the vibrational amplitude. The gravity acceleration in the co-moving frame of reference is g(t) = g(1 + αcos(ωt)), where α = is the dimensionless scaled amplitude. Since viscosity is neglected, we anticipate the onset of the subharmonic vibrations at small amplitude α ≪ 1. In this regime, we obtain from Eq. for the time-dependent squashing 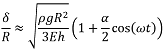. In this limit, Eq. reduces to the three-dimensional Mathieu function

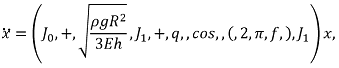(4)

where 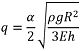is the scaled vibration amplitude.

We emphasise that the linear model Eq. can only be used for qualitative estimations of generally nonlinear subharmonic response. Discrepancies with experimental results obtained for real earthworms can be due to viscoelastic damping, nonlinear deformation and twisting of the worm body, as well as due to the assumption of a thin wall elastic cylinder filled with Newtonian fluid used in the model.

The properties of solutions of Eq. are well-known [68]. Parametrically excited instability sets in when 2πf coincides with one of the combination frequencies , where are the eigenvalues of 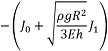. Because ∼0.04 for E = 1 MPa, we can neglect the term J₁ in Eq. as compared with J₀, which implies that the natural frequencies ω_0i of the gravity squashed worm can be approximated by those of a circular elastic cylinder.

Amongst the three frequencies (ω₀) one is typically two orders of magnitude lower than the other two. This lowest frequency ω₀ corresponds to the mode with predominantly radial displacement and is given by [64]

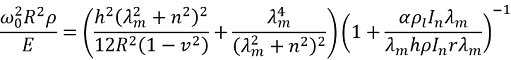(5)

where λ_m = and In is the modified Bessel function of the first kind of order n.

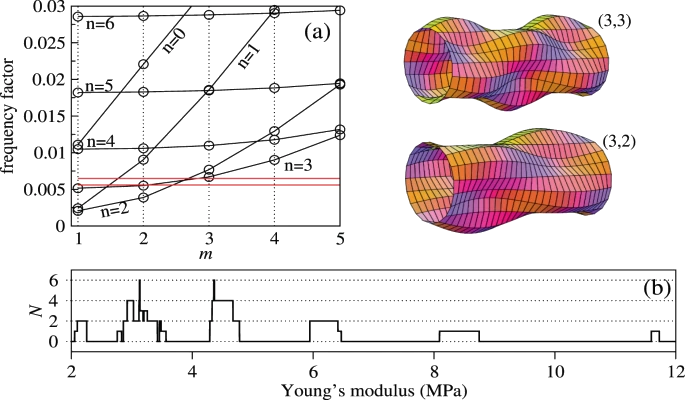
Considered as a whole, the combination ω₀R in Eq. depends on the geometry of the cylinder, the Poisson ratio ν and the ratio of the densities , but is independent of the Young’s modulus E. In Fig. 6, we plot the frequency factor as a function of the axial mode number m for different values of n for a cylinder of length L = 10 cm, shell thickness h = 50 μm, radius R = 5 mm, filled with a fluid with density ρ_l = ρ = 1100 ^kg/_m³. The first three lowest frequency modes with n = 1, m = 1, n = 2, m = 2 and n = 2, m = 1 are shown in the right panel of Fig. 5 for the sake of illustration.

Analysis of experimental results in light of the predictions of the developed theoretical model. By scanning through all theoretically possible combinations of vibration modes and varying the value of the effective Young’s modulus of the worm, we find the modes involved in the subharmonic response of the worm and plot the respective spatial mode profiles. (a) Frequency factor ω₀R plotted as a function of the axial mode number m for the circular elastic cylinder filled with liquid with density ρ_l. The other parameters are R = 5 mm, L = 10 cm, ρ = ρ_l = 1100 ^kg/_m³, ν = 0.5 and h = 50 μm. The circumferential mode number n is indicated next to each curve. The two solid horizontal lines correspond to the levels of 38πR and 43πR with E = 8.3 MPa. For E = 8.3 MPa, the mode n = 3, m = 3 is excited at 38 Hz and the mode n = 2, m = 3 is excited at 43 Hz. The frequencies 38 Hz and 43 Hz correspond to the first and the second minimum of the critical vibration amplitude function in Fig. 4. The number of modes N that match the subharmonic resonance criterion as a function of E. From this panel we obtain information about the largest possible values of the Young’s modulus corresponding to the modes at 38 Hz and 43 Hz.

Discussion

The presented theoretical model can, in general, be used to find the mode profiles corresponding to the resonance frequencies found in the experiment in Fig. 4 by using experimental data for the Young’s modulus E of earthworms as a key input parameter. However, plausible values of E for different worm species are a subject of active debate due to a large range of the reported values and poor understanding of the impact of the cuticle on mechanical properties of worms [53, 60].

To circumvent the lack of experimental data, we reanalyse our experimental results in Fig. 4 in light of the predictions of the developed model Eqs. In particular, we establish which of the theoretically possible vibrational modes could be excited at a given value of E. Here, we vary the value of E in a range bounded by two critical values – the effective bulk Young’s modulus of the worm from [53] and the locally measured stiffness of the cuticle [60, 61]. Whereas the exact values of E are yet to be confirmed experimentally, it has already been established that E would be a function of the thickness of the cuticle60 and that it would approach 200 … 400 MPa [61] in a limiting case of the mechanical properties of the worm defined solely by the cuticle.

Naturally, the thickness and stiffness of the cuticle vary for different species of worms and they are also likely to vary from one animal to another within the same species group. Indeed, in our experiments we established that Eisenia fetida earthworms appear to be slightly stiffer when palpated as compared with the other species tested in this work. However, this difference alone cannot result in an order of magnitude discrepancy in the values of E.