Три принципа научного эффектизма

Н.С. Приходченко, Е.И. Лубяницкий

УДК 338.94:83.3(2)1

Статья посвящена рассмотрению принципов научного эффектизма, науки, доступной для понимания и осмысления не только профессиональными экономистами, но и всеми научными сотрудниками, когда-либо открывавшими заказ-наряды на проведение научно-исследовательских работ в своей отрасли науки — будь то анодная защита металлов от коррозии, химическая технология или, в конце концов, технико-экономические исследования.

Итак, что же такое научный эффектизм?

Ни одна энциклопедия, ни один экономический справочник, изданные до настоящего времени, не смогут дать ответ на этот вопрос.

Общеизвестно, в настоящее время развитие науки и техники идет по пути открытия заказ-нарядов и проведении исследований в соответствии с утвержденными программами работ по данным заказ-нарядам с последующим их закрытием. Особое внимание при открытии того или иного заказ-наряда уделяется его эффектизации. До настоящего времени это было чисто технической стороной дела, но с ростом заказ-нарядизации, усложнением процедуры согласования и утверждения экономических эффектов и др. и пр. и т.д. и т.п. появилась необходимость создания теоретической базы, научного обоснования этого рода деятельности, которую мы назвали научным эффектизмом.

Научный эффектизм — это совокупность приемов и методов научного обоснования и определения размеров денежных вознаграждений за выполненную НИР, позволяющих исключить даже косвенный контакт с нормами Уголовного Кодекса

Предвидим возражения в наш адрес.

Во-первых, в 1977 издана утвержденная методика эффектизации. На ее основе разработаны отраслевые методики. Во-вторых, существуют инструкции, регламентирующие все этапы и процедуры заказ-нарядизации и др. и пр. и т.д. и т.п.

Да, это так. Но все эти нормативные документы недостаточно четко определяют цель проведения эффектизации НИР. В результате, и исследователь, и заказчик НИР используют эффектизацию только для эффектизма. Таким образом, мы вплотную приблизились к формулированию первого принципа научного эффектизма:

неясность цели эффектизации.

В этом, по нашему мнению, и заключена суть нового направления экономической науки.

Экстраполируя результаты многолетних наблюдений на ближайшую перспективу, мы пришли к выводу, что второй принцип научного эффектизма был сформулирован задолго до появления терминов эффектизация, заказ-нарядизация, эффектизм и др. и пр. и т.д. и т.п. Его определение мы нашли в источнике [1]:

На свой пай сам промышляй.

Всякий озаказ-наряженый исследователь должен руководствоваться этим принципом ибо никакая служба эффектизма на предприятии не может знать преимуществ научной разработки лучше разработчика. В этом мы видим простор для развития служб эффектизма на предприятиях и в учреждениях.

Третий принцип научного эффектизма основан на игре слов face — лицо [2] и ФЭС — фонды экономического стимулирования. Приведем его без соответствующего обоснования, предоставив это читателям, в надежде на то, что ценность исследования от этого не пострадает:

Не имей научный face, но имей побольше ФЭС

Вышесказанное позволяет сделать следующие выводы.

  1. Создано и дано четкое определение нового направление экономической науки — научного эффектизма. Это дает толчок развитию служб научного эффектизма в отраслевых экономических научно-исследовательских институтах, а также служб эффектизма — на предприятиях и в учреждениях.
  2. Сформулированы 3 принципа научного эффектизма:
    ✓ неясность цели эффектизации;
    ✓ на свой пай сам промышляй;
    ✓ не имей научный face, но имей побольше ФЭС.

Авторы, предвидя бурный рост количества исследований во вновь созданном направлении экономики, никоим образом не ограничивают количество основополагающих принципов научного эффектизма тремя вышеперечисленными.

Литература
  1. Пословицы русского народа: Сборник В.Даля. — М.: Художественная литература, 1984, т.1, с.378.
  2. Большой англо-русский словарь. — М.: Русский язык, 1979, т.1, с.484.

Текст публикуется по ТЧК

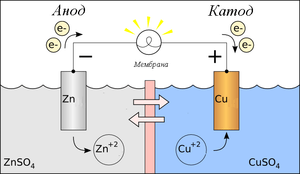
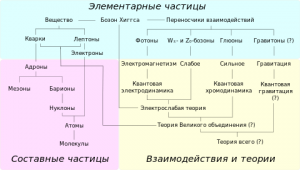
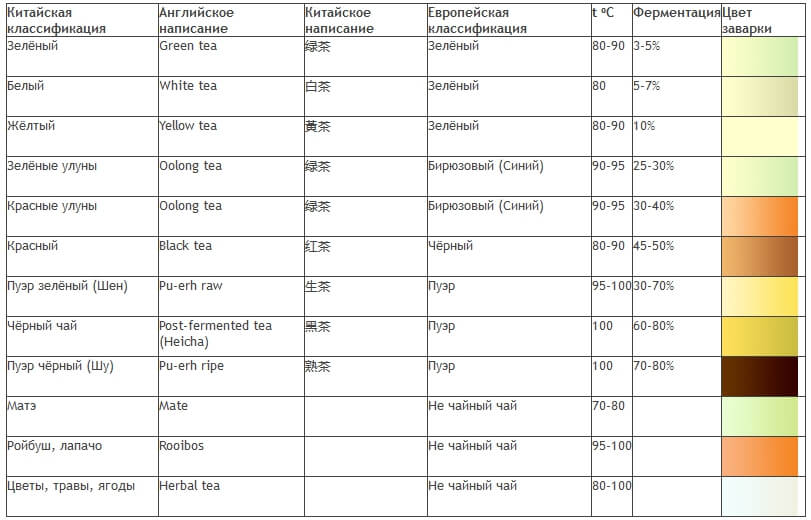
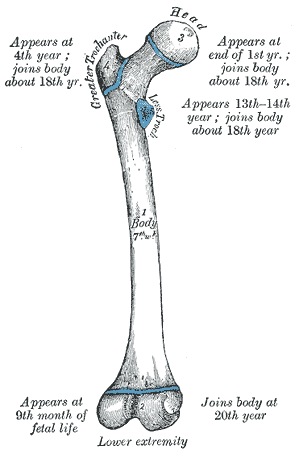
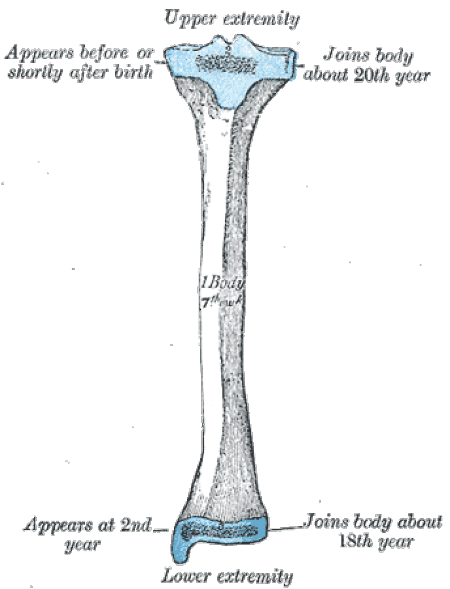
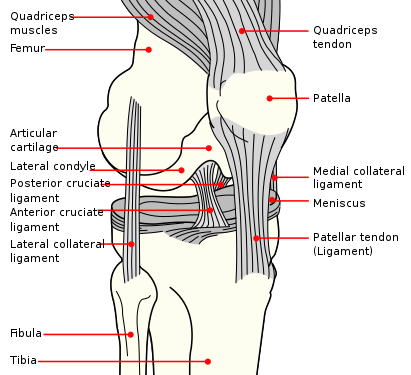
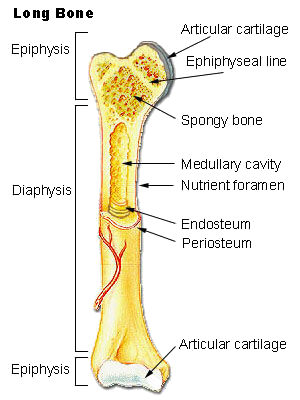
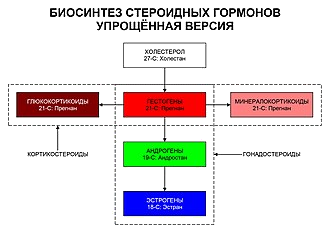
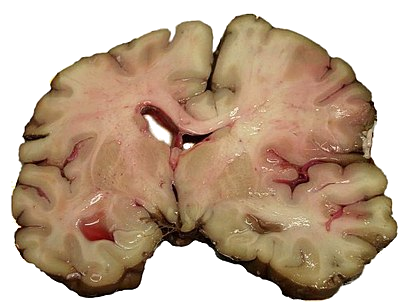
Когда верстался номер

     В редакцию пришло сообщение из Новосибирска. Журнал ЭКО принял статью авторов из Северодонецка Три принципа научного эффектизма для рассмотрения вопроса о возможности ее подготовки к публикации.
     Редколлегия поздравляет Н.С. Приходченко и Е.И. Лубяницкого и желает положительных результатов рассмотрения.
     Во втором томе мы опубликуем сообщение о публикации этой статьи.

Когда версталась страничка

     уже было известно об отказе в публикации. Основными причинами явились возможность публикации только в разделе Post Scriptum и недостаточная юмористичность.

Картинка: Ирина Зайцева

Омар Хайям
Продолжение. К началу.
Алгебраические решения производятся при помощи уравнения, т.е., как это хорошо известно, приравнения одних степеней другим.
     Словом, алгебра определяется как наука об уравнениях и именно о тех уравнениях, которые в настоящее время называются алгебраическими. Мы впервые здесь находим и термин алгебраисты — ал-джабриййуна.
     Задачей алгебры является определение как числовых, так и геометрических неизвестных. Здесь Хайям свидетельствует, что математики стран ислама занимались поисками числового решения кубического уравнения, т.е. решения в радикалах, но тщетно. О различных видах уравнений 3-й степени он пишет:
     Доказательство этих видов в том случае, когда предмет задачи есть абсолютное число, невозможно ни для нас, ни для кого из тех, кто владеет этим искусством. Может быть, кто-нибудь из тех, кто придет после нас, узнает это для случая, когда имеется не только три первых степени, а именно число, вещь и квадрат
     Такое решение кубического уравнения было найдено итальянцами в начале XVI в., через 400 лет после смерти Омара Хайяма.
     Другим важнейшим трудом Омара Хайяма — Комментарии к трудностям во введениях книги Евклида. Начала Евклида, появившиеся в первом арабском переводе ал-Хаджжаджа около 800, сыграли выдающуюся роль в развитии математики в странах ислама. Почти сразу они стали предметом комментирования, а затем и критики; ко времени Хайяма можно насчитать по крайней мере 30 арабских сочинений такого рода. Особенное внимание привлекали аксиоматика и определения I книги и основанная на V постулате теория параллельных, а также общая теория отношений V книги и теория квадратичных иррациональностей трудной Х книги.
     Комментарии Хайяма разделены на три книги, которым предшествует введение. Во введении автор говорит о предмете сочинения и некоторых своих предшественниках. Характерна высокая оценка философско-логических трудов Аристотеля. Омар Хайям не только принимает учение Аристотеля о структуре дедуктивной науки и его теорию доказательства, но следует за великим греком и в ряде более частных вопросов.
     В первой книге Комментариев изложена теория параллельных. Хайям, конечно, не сомневается в истинности классического постулата Евклида, но считает его менее очевидным, чем ряд предложений, которые Евклид считал нужным доказывать. вроде теоремы о том, что равные центральные углы высекают на окружностях равных кругов равные дуги. Хайям отвергает некоторые попытки доказать V постулат, например Герона, Евтокия, ан-Найризи, как логически несостоятельные. Он отвергает и доказательство Ибн ал-Хаисама, который в основу теории параллельных положил утверждение, что линия, описываемая верхним концом перпендикуляра данной длины при движении нижнего конца вдоль данной прямой, есть прямая. Это утверждение Ибн ал-Хайсам в своих Комментариях к введениям книги Евклида Начала пытался доказать при помощи некоторых неявных допущений относительно свойств равномерного прямолинейного движения. Омар Хайям не согласен с подходом Ибн ал-Хайсама в принципе, так как, вслед за Аристотелем, он исключает из геометрии определения такого рода, дающие место движению.
     Беда предшествующих ученых, по мнению Омара Хайяма, состоит в том, что они не учитывали принципов, заимствованных у философа, — имеются в виду принципы, выдвинутые Аристотелем. Один из этих принципов, которого, впрочем, в известных нам трудах Аристотеля не имеется, Хайям принимает за исходный в собственной теории параллельных: две сходящиеся прямые линии пересекаются, и невозможно, чтобы две сходящиеся прямые линии расходились в направлении схождения. Каждое из двух утверждений, содержащихся в принципе Аристотеля — Хайяма, эквивалентно V постулату.
     Вторая и третья книги Комментариев к трудностям во введениях книги Евклида посвящены теории отношений. И здесь Омару Хайяму предшествовал целый ряд ученых, комментировавших и отчасти критиковавших V книгу Начал.
     Хайям не отрицает правильности знаменитого определения тождества двух отношений в V книге «Начал», в котором сравниваются произвольные равнократные первой и третьей и, соответственно, второй и четвертой величин, образующих пропорцию. С его точки зрения это определение страдало, однако, важным пороком, ибо не раскрывало «истинный смысл пропорции». Мы бы сказали, что в глазах Хайяма это определение не выявляло измерительных свойств отношений, основных для математики стран ислама, в которой такое важное место занимали приближенные вычисления и действия с числовыми иррациональностями. Хайям стремился дать такое определение равенства отношений, которое непосредственно отражает числовую функцию отношения.
     Он хотел соединить общую теорию отношений V книги, пригодную и для непрерывных соизмеримых величин, и теорию отношений чисел VII книги. При этом Омар Хайям встал на путь, по которому, видимо, не шли его предшественники: он доказывает эквивалентность евклидовых определений тождества и неравенства отношений с новыми, — и это сразу освобождает его от вывода всех теорем V книги.
      

Добавить комментарий

Ваш адрес email не будет опубликован.