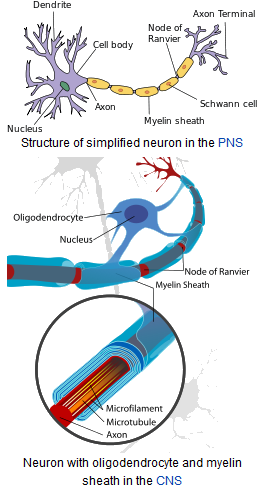
Ivan S. Maksymov, Andrey Pototsky Ivan S. Maksymov, Andrey Pototsky
The experiments were conducted by using the following protocol. The laser beam was focused on the body of the worm and the vibration amplitude of the Teflon plate was gradually increased until the point when the onset of Faraday instability was observed with the oscilloscope. The position of the worm was continually monitored with a digital camera to make sure that the same part of the worm is illuminated. Large vibration amplitudes leading to a horizontal displacement of the worm or jumps of the entire body were avoided to help keep the worm in the focus of the laser vibrometry setup. Large vibrations were also avoided because they additionally lead to ejection of a sticky fluid from the worm, which could serve as a medium for surface Faraday waves not wanted in our measurements. Typically, the total duration of measurements using the same worm was under five minutes to avoid desiccation. After the experiment, the worms were rehydrated and released into a worm farm. Figure 2 show, respectively, the vibration spectrum of the Teflon plate without the worm and the vibration spectrum of a Lumbricus terrestris earthworm placed horizontally on top of the Teflon plate. In both cases the Teflon plate is subjected to vertical vibration at f = 40 Hz.
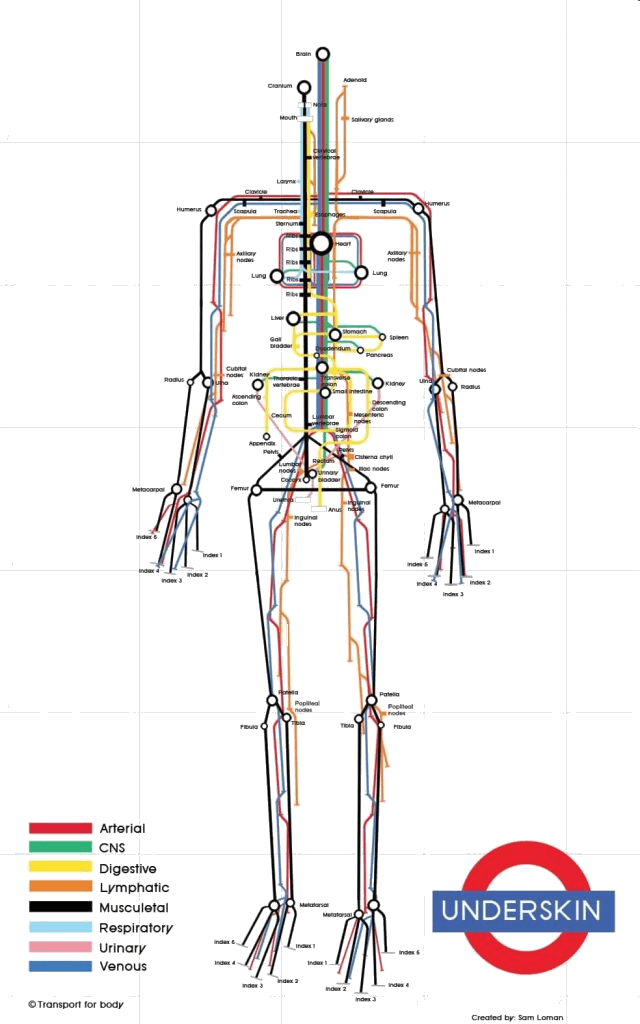
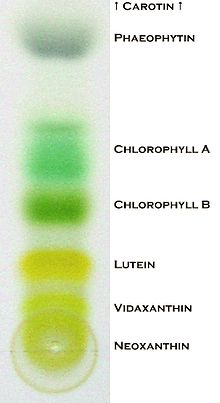
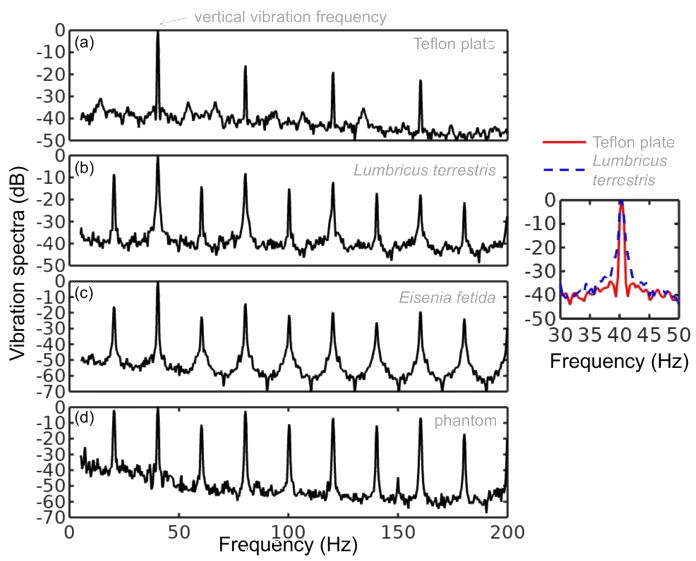 Vibration spectra of the Teflon plate without the worm, Lumbricus terrestris earthworm, Eisenia fetida earthworm and earthworm-mimicking phantom. The vertical vibration frequency is f = 40 Hz. All spectra are normalised to their respective maxima. Note the presence of subharmonic frequency peaks in the spectrum of the earthworms and the phantom, which are not present in the spectrum of the unloaded Teflon plate. The peaks in the spectrum of the earthworms are wider than in the case of the Teflon plate, which is a result of the amplitude modulation and appearance of frequency sidebands leading to the broadening of the peak [ 38]. Also note that the spectra of the worms and the worm-mimicking phantom are qualitatively similar. The vibration spectrum of the unloaded Teflon plate is dominated by the peak at the frequency f = 40 Hz and its higher-order harmonic frequencies 80, 120 and 160 Hz. The intensity of the second harmonic is approximately 50 times smaller than that of the fundamental signal and these signals are consistent with the intrinsic nonlinear distortion of the source of vertical vibrations used in our setup. We also calculated [47] that the fundamental natural vibration frequency of the Teflon plate is 43.7 Hz. The natural frequencies of the two higher order modes – 137.9 Hz and 294.9 Hz – are well above the vibration frequencies used in this work. This means that the vibration regime of the plate is far from the nearest antiresonance and that its frequency response is uniform in the frequency range of interest. In the vibration spectrum of the earthworm, we observe that the harmonic waves lose their stability via a period-doubling bifurcation [38] as evidenced by the appearance of the peaks at f = 20, 60, 140 and 180 Hz not present in the vibration spectrum of the Teflon plate. Significantly, the harmonic frequency peaks in the spectrum of the worm are wider as compared with the respective peaks in the spectrum of the Teflon plate. This is because the onset of subharmonic oscillations also results in the amplitude modulation and appearance of sidebands, which in turn leads to broadening of the spectral peaks previously reported for liquid films [20, 21] and liquid drops subjected to vibration [38]. Qualitatively the same behaviour is observed in the vibration spectrum of the other tested earthworm species, including the Eisenia fetida worms. We also note that the observed broadening effect cannot be attributed to the response of the Teflon plate. In general, broadening of spectral peaks of vibrated solid bodies can only be observed in the regime of extremely large vibration amplitudes not reached in our experiments. Experimental idealisation of a worm as an elongated liquid drop covered by a thin elastic skin is feasible because their water-filled body cavity is surrounded by a flexible skin and it acts as a hydrostatic skeleton [48]. The muscles of the worm are made of a viscoelastic material, but their volume is small as compared with that of the water-like liquid inside the body of the worm. Yet, when the worm is anaesthetised, its nervous system does not produce nerve impulses and therefore the muscles of its body are fully relaxed [14]. Consequently, the viscoelastic properties of the muscles can be neglected in the analysis of anaesthetised worms. Furthemore, whereas in non-anaesthetised worms high internal pressure helps to maintain a cylindrical shape [49], the pressure in anaesthetised worms is close to ambient [50]. We verified this by establishing that a puncture of the skin of an anaesthetised worm does not lead to a dramatic ejection of internal fluids typically seen in non-anaesthetised worms. To verify that an anaesthetised worm can be experimentally idealised as a water drop at ambient pressure enclosed by a thin elastic skin, we tested an earthworm-mimicking phantom made of a finger of an approximately 0.1-mm-thick latex glove filled with water. The thickness of the phantom wall is of the same order of magnitude as the body wall of an earthworm [51], but mechanical properties of latex films of sub-millimeter thickness [52] are similar to those of living worms [53]. The vibration spectrum of the phantom is shown in Fig. 2 and it is in good qualitative agreement with the vibration spectra of the real earthworms. Furthermore, in the following we assume that the body wall of the worm is an elastic cylindrical shell undergoing flexural vibrations. Direct mapping of flexural vibration modes with our laser vibrometry setup is currently unavailable. Thus, to demonstrate that the entire body of worm undergoes vibrations resulting in the appearance of subharmonic frequencies in the vibration spectrum, we use a time-domain approach. We first film worms vibrated at 40 Hz frequency with a digital camera capturing 120 frames per second and then we process the resulting videos in Octave software, where we binarise each frame and use the bwboundaries command to find the contours of the worm. Then, we calculate the area of the contour for every frame and we finally Fourier-transform the resulting area-versus-time dependence to obtain the vibration spectrum of the body of the worm.
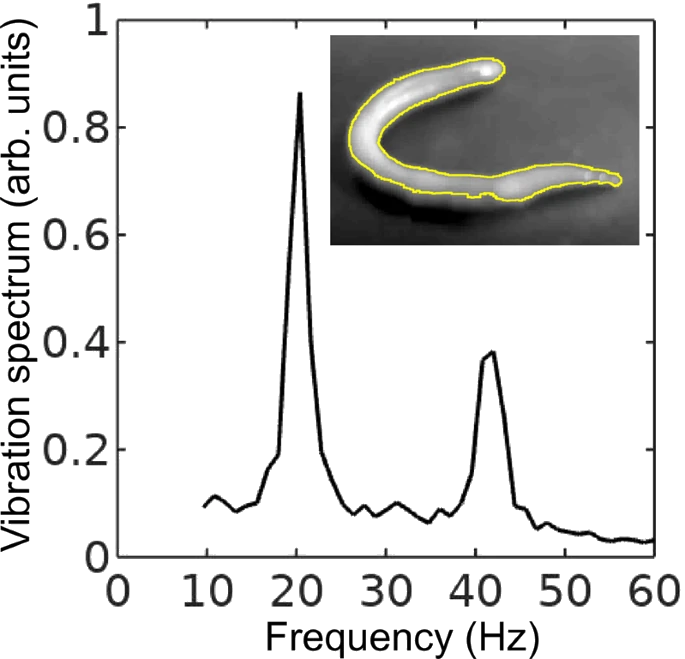 Vibration spectrum of the body of the earthworm subjected to vertical vibration at the frequency f = 40 Hz obtained by processing a video of the vibrated worm as explained in the main text. The subharmonic peak at 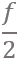 = 20 Hz can be clearly seen. The inset shows an example of the contour of the worm obtained from a single frame extracted from the video. As shown in Fig. 3, in agreement with the results obtained with the laser vibrometry setup, the body of the worm oscillates at the vibration frequency f ≈ 40 Hz and the subharmonic frequency 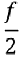 ≈ 20 Hz. However, whereas the spectra in Fig. 2 were obtained by focusing the laser beam on a part of the worm’s body, the spectrum in Fig. 3 originates from the vibrations of the entire body of the worm. The higher frequencies peaks present in Fig. 2 are not reproduced in Fig. 3, because the finite resolution and sample rate of the digital camera limit the resolving ability of the image processing based approach at higher frequencies. ≈ 20 Hz. However, whereas the spectra in Fig. 2 were obtained by focusing the laser beam on a part of the worm’s body, the spectrum in Fig. 3 originates from the vibrations of the entire body of the worm. The higher frequencies peaks present in Fig. 2 are not reproduced in Fig. 3, because the finite resolution and sample rate of the digital camera limit the resolving ability of the image processing based approach at higher frequencies.
 Ivan S. Maksymov, Andrey Pototsky. Excitation of Faraday-like Body Waves in Vibrated Living Earthworms. Page 1 2 3 4 5 | References48. Kier, W.M. The diversity of hydrostatic skeletons. J. Exp. Biol. 215, 1247 – 1257. ◄ ► 49. Harris, J. & Crofton, H. Structure and function in the nematodes: internal pressure and cuticular structure in Ascaris. J. Exp. Biol. 34, 116 – 130. ◄ 50. McKenzie, B.M. & Dexter, A.R. Physical properties of casts of the earthworm Aporrectodea rosea. Biol. Fertil. Soils 5, 152 – 157. ◄ 51. Briones, M.J.I. & Álvarez Otero, R. Body wall thickness as a potential functional trait for assigning earthworm species to ecological categories. Pedobiologia 67, 26 – 34. ◄ ► 52. Simchareon, W., Amnuaikit, T., Boonme, P., Taweepreda, W. & Pichayakorn, W. Characterization of natural rubber latex film containing various enhancers. Procedia Chem. 4, 308 – 312. ◄ 53. Backholm, M., Ryu, W.S. & Dalnoki-Veress, K. Viscoelastic properties of the nematode caenorhabditis elegans, a self-similar, shear-thinning worm. PNAS 110, 4528 – 4533. ◄ ► ► ► ► ► ► ► ► 54. Ballesta, P. & Manneville, S. Signature of elasticity in the Faraday instability. Phys. Rev. E 71, 026308. ► ► 55. Maity, D.K., Kumar, K. & Khastgir, S.P. Instability of a horizontal water half-cylinder under vertical vibration. Exp. Fluids 61, 25. ► ► ► 56. Wang, C.Y. & Watson, L.T. The fluid-filled cylindrical membrane container. J. Eng. Math. 15, 81 – 88. ► 57. Hidaka, T., Kuriyama, H. & Yamamoto, T. The mechanical properties of the longitudinal muscle in the earthworm. J. Exp. Biol. 50, 431 – 443. ► 58. Tashiro, N. Mechanical properties of the longitudinal and circular muscle in the earthworm. J. Exp. Biol. 54, 101 – 110. ► 59. Colbert, M.-J., Raegen, A., Fradin, C. & Dalnoki-Veress, K. Adhesion and membrane tension of single vesicles and living cells using a micropipette-based technique. Eur. Phys. J. E 30, 117 – 121. ► 60. Gilpin, W., Uppaluri, S. & Brangwynne, C.P. Worms under pressure: Bulk mechanical properties of C. elegans are independent of the cuticle. Biophys. J. 108, 1887 – 1898. ► ► ► ► ► ► ► 61. Nakajima, M., Ahmad, M.R., Kojima, S., Homma, M. & Fukuda, T. Local stiffness measurements of C. elegans by buckling nanoprobes inside an environmental sem. In 2009 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, 4695 – 4700. ► ► ► ► ► 62. Arnold, R.N., Warburton, G.B. & Born, M. Flexural vibrations of the walls of thin cylindrical shells having freely supported ends. Proc. Royal Soc. Lond. A 197, 238 – 256. ► 63. Warburton, G.B. Vibration of thin cylindrical shells. J. Mech. Eng. Sci.7, 399 – 407. ► 64. Lindholm, U.S., Kana, D.D. & Abramson, H.N. Breathing vibrations of a circular cylindrical shell with an internal liquid. J. Aerospace Sci. 29, 1052 – 1059. ► ► 65. Amabili, M. Theory and experiments for large-amplitude vibrations of empty and fluid-filled circular cylindrical shells with imperfections. J. Sound Vib. 262, 921 – 975. ► 66. Amabili, M. Nonlinear Mechanics of Shells and Plates in Composite, Soft and Biological Materials. Cambridge University Press. ► 67. Shirakawa, K. & Morita, M. Vibration and buckling of cylinders with elliptical cross section. J. Sound Vib. 84, 121 – 131. ► 68. Hsu, C. On the parametric excitation of a dynamic system having multiple degrees of freedom. J. Appl. Mech. 30, 367 – 372. ► 69. Maksymov, I.S. Faraday waves in earthworms: non-invasive tests of the soliton model of nerve impulses. In Proc. 12th Australasian Workshop on Computational Neuroscience and Neural Engineering, 12 (2019). ► 70. Julian, F.J. & Coldman, D.E. The effects of mechanical stimulation on some electrical properties of axons. J. Gen. Physiol. 46, 297 – 313. ► 71. Berry, J.G. & Reissner, E. The effect of an internal compressible fluid column on the breathing vibrations of a thin pressurized cylindrical shell. J. Aerosp. Sci. 25, 288 – 294. ► George W. Hart. Mathematically Correct BreakfastHow to Slice a Bagel into Two Linked Halves
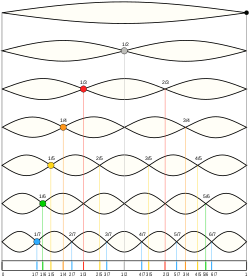
It is not hard to cut a bagel into two equal halves which are linked like two links of a chain. 
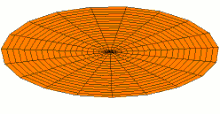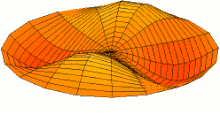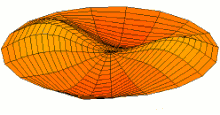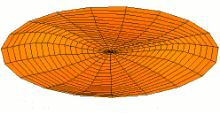
To start, you must visualize four key points. Center the bagel at the origin, circling the Z axis. A is the highest point above the +X axis. B is where the +Y axis enters the bagel. C is the lowest point below the —X axis. D is where the —Y axis exits the bagel. 
These sharpie markings on the bagel are just to help visualize the geometry and the points. You don’t need to actually write on the bagel to cut it properly. 
The line ABCDA, which goes smoothly through all four key points, is the cut line. As it goes 360° around the Z axis, it also goes 360° around the bagel. 
The red line is like the black line but is rotated 180°. An ideal knife could enter on the black line and come out exactly opposite, on the red line. But in practice, it is easier to cut in halfway on both the black line and the red line. The cutting surface is a two-twist Mobius strip; it has two sides, one for each half. |