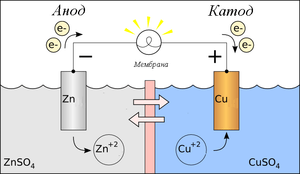
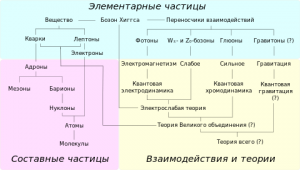
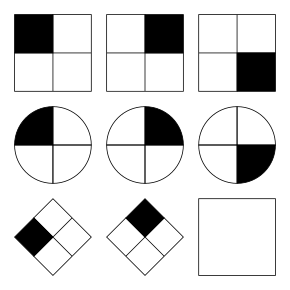
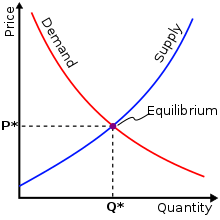
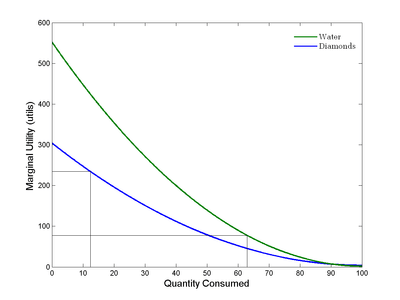
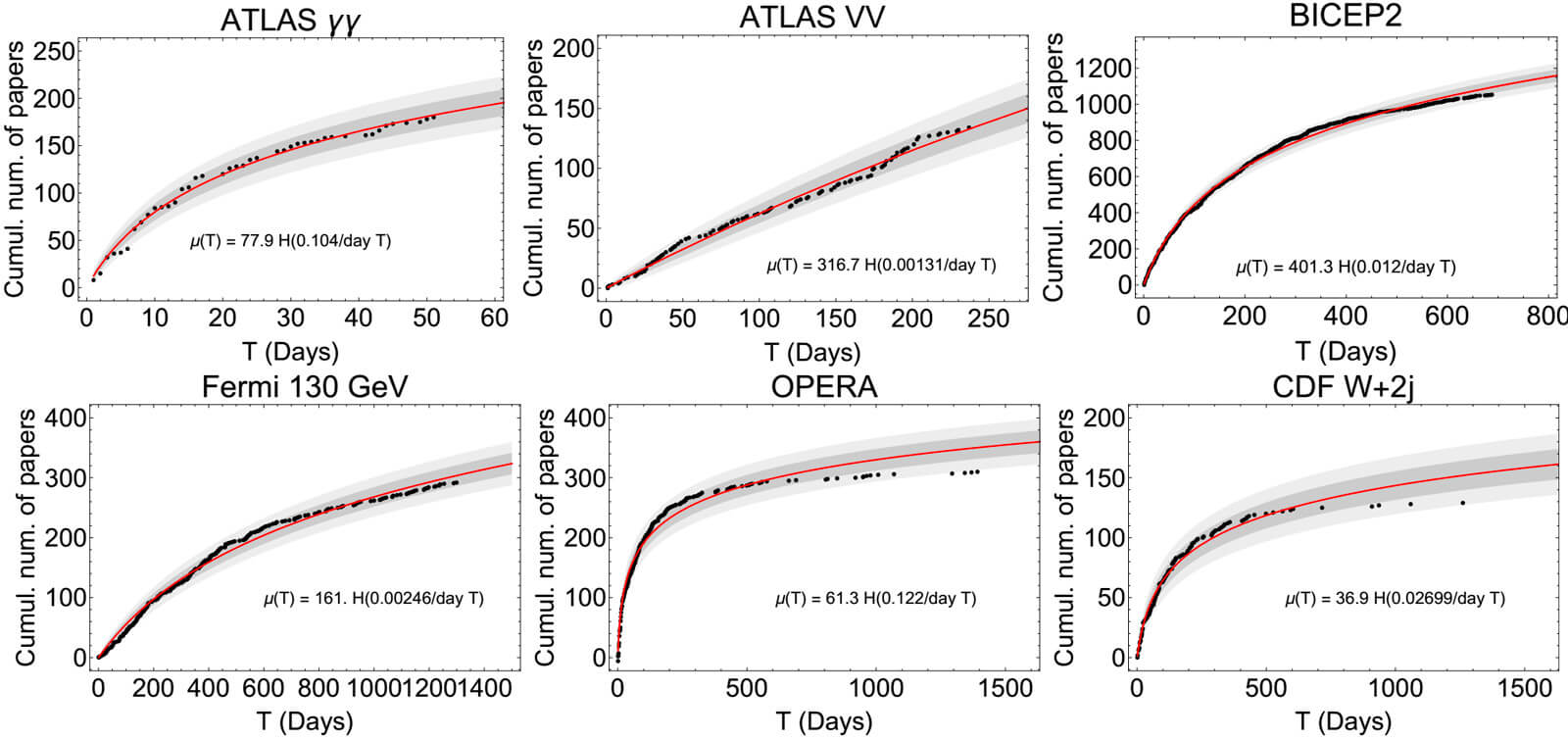
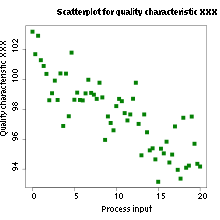
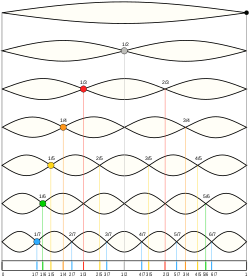
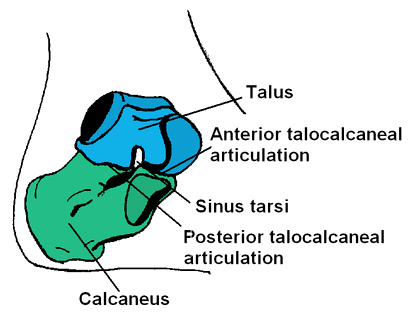
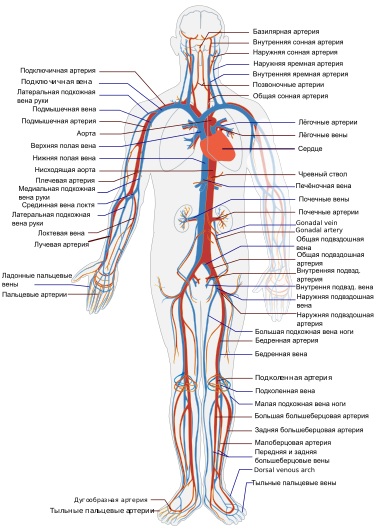
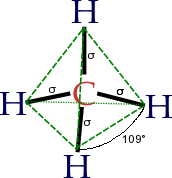
| 25 лет теории теорийПослесловие издателя С момента выхода статьи Б.Н. Волгина миновала четверть века, но теория теорий жива! Ею пользуются члены и члены-корреспонденты Чайного Клуба, авторы и, возможно, читатели. Редакция ТЧК также часто обращается к ее постулатам. Уважаемые члены и члены-корреспонденты Чайного Клуба, уважаемые авторы и читатели! Мы обращаемся к вам с просьбой. До сих пор не найден основатель бессмертной теории теорий Борис Николаевич Волгин! Публикация теория теорий в журнале ЭКО и в ТЧК дала путевку в жизнь только на страницах нашего издания 12 новым направлениям в Науке! Если вам известны какие-либо координаты Б.Н. Волгина, будьте любезны, сообщите их нам! Даже обращение в редакцию ЭКО нам не помогло. Страна должна знать своих героев! И в XXI веке нашлись ее ценители и продолжатели. Свидетельства тому — как научная деятельность вполне серьезных ученых, так и развитие паранаучной терминологии уже после выхода в свет теории теорий. В преддверии 20-летия ТЧК, которое будет отмечаться в День Знаний, 1 сентября 2006 г., это обстоятельство убеждает нас в правильности выбранного, как модно сейчас говорить, формата нашего издания и необходимости продолжения паранаучной деятельности. К сожалению, офф-лайновая версия ТЧК уже — музейный раритет. 24 Feb 06 И вдогонку событию нам пишет Дорогая Редакция: А вот ссылка на тему Как изложить полученные результаты и подготовить научную публикацию, доклад или любое другое обращение к коллегам? — http://vivovoco.astronet.ru/VV/PAPERS/SCILANG/SCILANG.HTM. 27 Mar 07 Как говорится, to be continued: В ЖЖ натыкаюсь, конечно, не на теорию теорий, но вполне серьезное, а главное, — самостоятельное исследование молодой ученой Р. Барракуды по теме, исследовавшейся еще в прошлом веке Б.Н. Волгиным, Дж.Б.С. Холдейном. Указ о ее награждении уже подписан. 16 Nov 10 Заметки на полях— это приглашение к разговору. Мы предлагаем рассказать: ✓ о своих первых математических впечатлениях, ✓ о том, что, по твоему мнению, представляют собой производная, математика, аналитическая геометрия, аксиоматика, ✓ высказаться по поводу площади круга и его частей. Мы предлагаем решить в общем виде задачу о поимке льва в пустыне. В надежде на заинтересованность и любовь к математике, научным знаниям вообще, мы ждем от тебя статей и заметок, отзывов и предложений. Лорд Кельвин о производной Войдя раз в аудиторию, Томсон обратился к слушателям с вопросом: что такое dx/dt? В ответ он получил все мыслимые строго логические определения. Все они были отвергнуты: — Ах, бросьте вы этого Тодгентера, dx/dt есть скорость! Текст публикуется по Ф. Клейн. Лекции о развитии математики в XIX столетии Альберт Эйнштейн о своих первых математических впечатлениях …В возрасте 12 лет я пережил еще одно чудо совсем другого рода: источником его была книжечка по евклидовой геометрии на плоскости, которая попалась мне в руки в начале учебного года. Там были утверждения, например, о пересечении трех высот треугольника в одной точке, которые хотя и не были сами по себе очевидны, но могли быть доказаны с уверенностью, исключавшей, как будто, всякие сомнения. Эта ясность и уверенность произвела на меня неописуемое впечатление. Меня не беспокоило то, что аксиомы должны быть приняты без доказательства. Вообще мне было достаточно, если я мог в своих доказательствах опираться на такие положения, справедливость которых представлялась мне бесспорной. Я помню, например, что теорема Пифагора была мне показана моим дядей еще до того, как в мои руки попала священная книжечка по геометрии. С большим трудом мне удалось «доказать» эту теорему при помощи подобных треугольников; при этом, однако, мне казалось «очевидным», что отношение сторон прямоугольного треугольника должно полностью определяться одним из его острых углов. Вообще мне казалось, что доказывать нужно только то, что не «очевидно» в этом смысле… …В возрасте 12 — 16 лет я ознакомился с элементами математики, включая основы дифференциального и интегрального исчисления. При этом, на мое счастье, мне попались книги, в которых обращалось не слишком много внимания на логическую строгость, зато хорошо была выделена главная мысль. Все это занятие было поистине увлекательно; в нем были взлеты, по силе впечатления не уступавшие «чуду» элементарной геометрии — основная идея аналитической геометрии, бесконечные ряды, понятие дифференциала и интеграла… Текст публикуется по Альберт Эйнштейн. Творческая биография Мария Брановская о математике Сложить и вычесть — это математика. Что сложить и что вычесть — это уже не математика Максим Музыка. Люблю математику Премия за подбитый танк — 48720 грн. Масса танка Т-72 — 41 тонна. Цена металлолома ~3000 грн/тонна Цена танка при сдаче в металлолом — 123000 грн. Кое-кто знает толк в коммерции. Текст публикуется по Факты Вирус. Что такое математика Математика — это наука, исторически основанная на решении задач о количественных и пространственных соотношениях реального мира путём идеализации необходимых для этого свойств объектов и формализации этих задач. В современной математике идеализированные свойства исследуемых объектов и процессов формулируются в виде аксиом, затем по строгим правилам логического вывода из них выводятся другие истинные свойства. Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики. Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причем некоторые из них занимают пограничное к математике положение — в частности, формальная логика может рассматриваться и как часть философских наук и как часть математических наук, механика – и физика и математика, программирование, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т.д. В литературе было предложено много различных определений математики. Слово математика произошло от греч. µαθηµα, означающего «науку, знание, изучение», и греч. µαθηµατικος, означающего любовь к познанию. Текст публикуется по @Ответы Акад. А.Н. Колмогоров об аксиоматике Мне представляется единственно удачным выходом сопоставить те общие свойства длин, площадей и объемов, которые позволяют выразить их при выбранной единице меры числами, и называть системой величин всякую совокупность объектов, обладающую этими свойствами. Но это уже не что иное, как аксиоматический метод, который не должен казаться скомпрометированным своей связью с конвенционализмом. Действительно, когда Гильберт в Основаниях геометрии предлагает называть пространством любую совокупность объектов и отношений, удовлетворяющую его аксиомам, то вместе с Лебегом следует протестовать, если из определения Гильберта делают заключение о произвольности выбора объекта изучения в математике. Однако то же самое определение Гильберта можно воспринимать совсем противоположным образом. Можно утверждать, что система аксиом, лежащих в основе геометрии, является замечательным, концентрированным выражением результата наших усилий, направленных к познанию действительности. Успех, заключающийся в ее создании, тем более замечателен, что она не только отражает с очень большой точностью свойства окружающего нас пространства при обычной интерпретации ее основных понятий, но также хорошо приспособлена и для выражения совсем других закономерностей внешнего мира при других ее интерпретациях. Таким образом, абстрактная геометрия больше связана с действительностью, чем геометрия в ее традиционной форме. Текст публикуется по Лебег А. Об измерении величин А. Лебег о площади круга и его частей Раньше, например, в пору моего детства, простосердечно говорили, что так как многоугольники p отличаются все меньше и меньше от круга, то площадь круга есть предел площадей p. О площади, рассматриваемой как первичное понятие, рассуждали одинаково хорошо как в случае круга, так и в случае многоугольников, и опирались на несформулированные и молчаливо предполагаемые свойства этих площадей. Конечно, с точки зрения логической это было недостаточно; однако оказывалось, что ничего неприемлемого не говорилось, тогда как нынешнее изложение совершает, по-моему, больший грех если не против логики, то что еще хуже, против здравого смысла. Заодно обнаруживают наивное легковерие во всемогущество слова, заставляющее надеяться, что затруднение будет побеждено искусством речи. Как будто бы настоящий прогресс может быть достигнут столь дешевой ценой! В самом деле, как поступают в настоящее время? Площадь круга есть предел p. Это есть произвольное определение, название, которое может быть заменено всяким другим. Отсюда следует, что недостаточно еще принять это, а не другое, название, чтобы число, названное таким образом, площадью круга, поспешило благоразумно войти в семейство тех чисел, для которых справедливы свойства а), б), в), г). В результате этого из известной формы для площади круга нельзя логически вывести формулу площади сектора; верить в это и пускаться в мнимые рассуждения, значит глубоко заблуждаться. Площадь сектора равна
по определению. Из площади сектора, принятой, таким образом, по определению, нельзя вывести путем рассуждения площади сегмента; опять-таки определением является то, что площадь сегмента равна разности между площадью сектора и площадью треугольника. Если бы предел p был назван тарарабумбией круга, то вряд ли кто-нибудь позволил вывести из нее величину тарарабумбий сектора и сегмента; но делать это разрешают себе, когда вместо слова тарарабумбия употребили слово площадь! Это — тягчайшее преступление против здравого смысла. Однако иные находят оправдание в том, что они сами этой ошибки не совершают, но делают ставку на то смешение, которое не замедлят совершить учащиеся, уподобляя эту новую площадь тем площадям, с которыми они привыкли иметь дело. Каждому, впрочем, предоставляется возможность выбирать между заблуждением и лицемерием. Пусть не надеются, к тому же, выйти из затруднительного положения, повторяя три раза, по случаю круга, сектора и сегмента, вещие слова по определению, так как определенные таким путем площади ни к чему не пригодны. С их помощью нельзя разрешить ни одного вопроса, ни одной проблемы без того, чтобы не натолкнуться на предложения а), б), в), г), пользоваться которыми будет незаконно; так, например, не мог быть рассмотрен классический пример о луночках Гиппократа. Текст публикуется по Лебег А. Об измерении величин Эдгар По о квадратном уравнении Известный американский писатель Эдгар По получил высшее математическое образование. В одном из своих рассказов он тонко подметил одно из тех заблуждений, которые распространены в широкой публике из-за неверного понимания истинного смысла математических формул.
Текст публикуется по Э. По. Украденное письмо, переведенное К.Д.Бальмонтом. Случай с Дедекиндом Автор наиболее широко распространенной теории иррациональных чисел Р. Дедекинд умер, как известно, 12 февраля 1916 в возрасте 84 лет. Однако еще в 1904 в Книжке памятных дат для математиков, опубликованной в качестве приложения к каталогу издательства Тейбнер и предназначенной для участников III Международного математического конгресса, состоявшегося в Гейдельберге в том же году, был отмечен под датой 4 сентября 1899 …день смерти Р. Дедекинда. Последний не замедлил написать письмо составителю упомянутой книжки примерно следующего содержания:
Текст публикуется по Рассказы, истории, байки, легенды, а также. |